【题目】如图2,“六芒星”是由两个全等正三角形组成,中心重合于点O且三组对边分别平行.点A,B是“六芒星”(如图1)的两个顶点,动点P在“六芒星”上(内部以及边界),若 ![]() ,则x+y的取值范围是( )
,则x+y的取值范围是( ) 
A.[﹣4,4]
B.![]()
C.[﹣5,5]
D.[﹣6,6]
参考答案:
【答案】C
【解析】解:设 ![]() =
= ![]() ﹐
﹐ ![]() =
= ![]() ﹐求x+y的最大值﹐只需考虑右图中6个顶点的向量即可,
﹐求x+y的最大值﹐只需考虑右图中6个顶点的向量即可, 
讨论如下﹔(1)∵ ![]() =
= ![]() ﹐∴(x,y)=(1,0);(2)∵
﹐∴(x,y)=(1,0);(2)∵ ![]() =
= ![]() +
+ ![]() =
= ![]() +3
+3 ![]() ﹐∴(x,y)=(3,1);(3)∵
﹐∴(x,y)=(3,1);(3)∵ ![]() =
= ![]() +
+ ![]() =
= ![]() +2
+2 ![]() ﹐∴(x,y)=(2,1); (4)∵
﹐∴(x,y)=(2,1); (4)∵ ![]() =
= ![]() +
+ ![]() +
+ ![]() =
= ![]() +
+ ![]() +(
+( ![]() +2
+2 ![]() )=3
)=3 ![]() +3
+3 ![]() ,∴(x,y)=(3,2); (5)∵
,∴(x,y)=(3,2); (5)∵ ![]() =
= ![]() +
+ ![]() =
= ![]() +
+ ![]() ﹐∴(x,y)=(1,1); (6)∵
﹐∴(x,y)=(1,1); (6)∵ ![]() =
= ![]() ﹐∴(x,y)=(0,1)
﹐∴(x,y)=(0,1)
∴x+y的最大值为3+2=5﹒
根据其对称性,可知x+y的最小值为﹣5﹒
故x+y的取值范围是[﹣5,5],
故选:C.
【考点精析】本题主要考查了平面向量的基本定理及其意义的相关知识点,需要掌握如果![]() 、
、![]() 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量
是同一平面内的两个不共线向量,那么对于这一平面内的任意向量![]() ,有且只有一对实数
,有且只有一对实数![]() 、
、![]() ,使
,使![]() 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系.若直线l的极坐标方程为
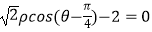 ,曲线C的极坐标方程为:ρsin2θ=cosθ,将曲线C上所有点的横坐标缩短为原来的一半,纵坐标不变,然后再向右平移一个单位得到曲线C1 . (Ⅰ)求曲线C1的直角坐标方程;
,曲线C的极坐标方程为:ρsin2θ=cosθ,将曲线C上所有点的横坐标缩短为原来的一半,纵坐标不变,然后再向右平移一个单位得到曲线C1 . (Ⅰ)求曲线C1的直角坐标方程;
(Ⅱ)已知直线l与曲线C1交于A,B两点,点P(2,0),求|PA|+|PB|的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|2x﹣a|+|2x﹣1|,a∈R. (I)当a=3时,求关于x的不等式f(x)≤6的解集;
(II)当x∈R时,f(x)≥a2﹣a﹣13,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】过双曲线x2﹣
 =1的右支上一点P,分别向圆C1:(x+4)2+y2=4和圆C2:(x﹣4)2+y2=1作切线,切点分别为M,N,则|PM|2﹣|PN|2的最小值为( )
=1的右支上一点P,分别向圆C1:(x+4)2+y2=4和圆C2:(x﹣4)2+y2=1作切线,切点分别为M,N,则|PM|2﹣|PN|2的最小值为( )
A.10
B.13
C.16
D.19 -
科目: 来源: 题型:
查看答案和解析>>【题目】设四棱锥P﹣ABCD的底面不是平行四边形,用平面 α去截此四棱锥,使得截面四边形是平行四边形,则这样的平面α( )

A.不存在
B.只有1个
C.恰有4个
D.有无数多个 -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 ,则f(x)在[0,k]的最大值h(k)=( )
,则f(x)在[0,k]的最大值h(k)=( )
A.2ln2﹣2﹣(ln2)3
B.﹣1
C.2ln2﹣2﹣(ln2)2k
D.(k﹣1)ek﹣k3 -
科目: 来源: 题型:
查看答案和解析>>【题目】5支篮球队进行单循环比赛(任两支球队恰进行一场比赛),任两支球队之间胜率都是
 .单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.有下列四个命题:p1:恰有四支球队并列第一名为不可能事件;p2:有可能出现恰有两支球队并列第一名;p3:每支球队都既有胜又有败的概率为
.单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.有下列四个命题:p1:恰有四支球队并列第一名为不可能事件;p2:有可能出现恰有两支球队并列第一名;p3:每支球队都既有胜又有败的概率为  ;p4:五支球队成绩并列第一名的概率为
;p4:五支球队成绩并列第一名的概率为  .其中真命题是( )
.其中真命题是( )
A.p1 , p2 , p3
B.p1 , p2 , p4
C.p1 , p3 , p4
D.p2 , p3 , p4
相关试题

