【题目】如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连接OB、OC.若∠BAC与∠BOC互补,则弦BC的长为( ) 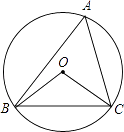
A.4 ![]()
B.3 ![]()
C.2 ![]()
D.![]()
参考答案:
【答案】C
【解析】解∵∠BAC与∠BOC互补,
∴∠BAC+∠BOC=180°,
∵∠BAC= ![]() ∠BOC,
∠BOC,
∴∠BOC=120°,
过O作OD⊥BC,垂足为D,
∴BD=CD,
∵OB=OC,
∴OB平分∠BOC,
∴∠DOC= ![]() ∠BOC=60°,
∠BOC=60°,
∴∠OCD=90°﹣60°=30°,
在Rt△DOC中,OC=2,
∴OD=1,
∴DC= ![]() ,
,
∴BC=2DC=2 ![]() ,
,
故选C.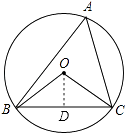
【考点精析】关于本题考查的垂径定理和三角形的外接圆与外心,需要了解垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,△ABE经旋转,可与△CBF重合,AE的延长线交FC于点M,以下结论正确的是( )

A.AM⊥FC
B.BF⊥CF
C.BE=CE
D.FM=MC -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连接OB、OC.若∠BAC与∠BOC互补,则弦BC的长为( )

A.4
B.3
C.2
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,△ABE经旋转,可与△CBF重合,AE的延长线交FC于点M,以下结论正确的是( )

A.AM⊥FC
B.BF⊥CF
C.BE=CE
D.FM=MC -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△OAB的顶点A(﹣4,8)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为6,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=2,则FM的长为 .
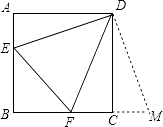
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△OAB的顶点A(﹣4,8)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为

相关试题

