【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(3,0),B(﹣1,0),C(0,﹣3).
(1)求该抛物线的解析式;
(2)若以点A为圆心的圆与直线BC相切于点M,求切点M的坐标;
(3)若点Q在x轴上,点P在抛物线上,是否存在以点B,C,Q,P为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)y=x2﹣2x﹣3;(2)M(﹣![]() ,﹣
,﹣![]() );(3)存在以点B,C,Q,P为顶点的四边形是平行四边形,P的坐标为(1+
);(3)存在以点B,C,Q,P为顶点的四边形是平行四边形,P的坐标为(1+![]() ,3)或(1﹣
,3)或(1﹣![]() ,3)或(2,﹣3).
,3)或(2,﹣3).
【解析】
(1)把A,B,C的坐标代入抛物线解析式求出a,b,c的值即可;
(2)由题意得到直线BC与直线AM垂直,求出直线BC解析式,确定出直线AM中k的值,利用待定系数法求出直线AM解析式,联立求出M坐标即可;
(3)存在以点B,C,Q,P为顶点的四边形是平行四边形,分两种情况,利用平移规律确定出P的坐标即可.
(1)把A(3,0),B(﹣1,0),C(0,﹣3)代入抛物线解析式得: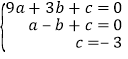 ,
,
解得: ,
,
则该抛物线解析式为y=x2﹣2x﹣3;
(2)设直线BC解析式为y=kx﹣3,
把B(﹣1,0)代入得:﹣k﹣3=0,即k=﹣3,
∴直线BC解析式为y=﹣3x﹣3,
∴直线AM解析式为y=![]() x+m,
x+m,
把A(3,0)代入得:1+m=0,即m=﹣1,
∴直线AM解析式为y=![]() x﹣1,
x﹣1,
联立得: ,
,
解得: ,
,
则M(﹣![]() ,﹣
,﹣![]() );
);
(3)存在以点B,C,Q,P为顶点的四边形是平行四边形,
分两种情况考虑:
设Q(x,0),P(m,m2﹣2m﹣3),
当四边形BCQP为平行四边形时,由B(﹣1,0),C(0,﹣3),
根据平移规律得:﹣1+x=0+m,0+0=﹣3+m2﹣2m﹣3,
解得:m=1±![]() ,x=2±
,x=2±![]() ,
,
当m=1+![]() 时,m2﹣2m﹣3=8+2
时,m2﹣2m﹣3=8+2![]() ﹣2﹣2
﹣2﹣2![]() ﹣3=3,即P(1+
﹣3=3,即P(1+![]() ,3);
,3);
当m=1﹣![]() 时,m2﹣2m﹣3=8﹣2
时,m2﹣2m﹣3=8﹣2![]() ﹣2+2
﹣2+2![]() ﹣3=3,即P(1﹣
﹣3=3,即P(1﹣![]() ,3);
,3);
当四边形BCPQ为平行四边形时,由B(﹣1,0),C(0,﹣3),
根据平移规律得:﹣1+m=0+x,0+m2﹣2m﹣3=﹣3+0,
解得:m=0或2,
当m=0时,P(0,﹣3)(舍去);当m=2时,P(2,﹣3),
综上,存在以点B,C,Q,P为顶点的四边形是平行四边形,P的坐标为(1+![]() ,3)或(1﹣
,3)或(1﹣![]() ,3)或(2,﹣3).
,3)或(2,﹣3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, 垂直平分
垂直平分 ,分别交
,分别交 、
、 于点
于点 、
、 ,
, 垂直平分
垂直平分 ,分别交
,分别交 ,
, 于点
于点 、
、 .
.⑴如图①,若
 ,求
,求 的度数;
的度数;⑵如图②,若
 ,求
,求 的度数;
的度数;⑶若

 ,直接写出用
,直接写出用 表示
表示 大小的代数式.
大小的代数式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】知识背景
当a>0且x>0时,因为(
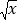 ﹣
﹣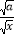 )2≥0,所以x﹣2
)2≥0,所以x﹣2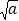 +
+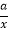 ≥0,从而x+
≥0,从而x+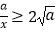 (当x=
(当x=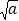 时取等号).
时取等号).设函数y=x+
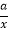 (a>0,x>0),由上述结论可知:当x=
(a>0,x>0),由上述结论可知:当x=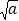 时,该函数有最小值为2
时,该函数有最小值为2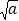 .
.应用举例
已知函数为y1=x(x>0)与函数y2=
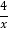 (x>0),则当x=
(x>0),则当x=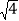 =2时,y1+y2=x+
=2时,y1+y2=x+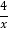 有最小值为2
有最小值为2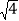 =4.
=4.解决问题
(1)已知函数为y1=x+3(x>﹣3)与函数y2=(x+3)2+9(x>﹣3),当x取何值时,
 有最小值?最小值是多少?
有最小值?最小值是多少?(2)已知某设备租赁使用成本包含以下三部分:一是设备的安装调试费用,共490元;二是设备的租赁使用费用,每天200元;三是设备的折旧费用,它与使用天数的平方成正比,比例系数为0.001.若设该设备的租赁使用天数为x天,则当x取何值时,该设备平均每天的租货使用成本最低?最低是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰△ABC中,AB=AC,∠ACB=72°,

(1)若BD⊥AC于D,求∠ABD的度数;
(2)若CE平分∠ACB,求证:AE=BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用若干个形状、大小完全相同的矩形纸片围成正方形,4个矩形纸片围成如图①所示的正方形,其阴影部分的面积为12;8个矩形纸片围成如图②所示的正方形,其阴影部分的面积为8;12个矩形纸片围成如图③所示的正方形,其阴影部分的面积为__.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个边长为 1 的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形, 其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了下图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了 2019 次后形成的图形中所有的正方形的面积和是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,AB=BC=4,把△ABC沿AC翻折得到△ADC.则
(1)四边形ABCD是 形;
(2)若∠B=120°,点P、E、F分别为线段AC、AD、DC上的任意1点,则PE+PF的最小值为 .

相关试题

