搜索
【题目】用若干个形状、大小完全相同的矩形纸片围成正方形，4个矩形纸片围成如图①所示的正方形，其阴影部分的面积为12；8个矩形纸片围成如图②所示的正方形，其阴影部分的面积为8；12个矩形纸片围成如图③所示的正方形，其阴影部分的面积为__．
参考答案：
【答案】44﹣16
．
【解析】图①中阴影部分的边长为
=2
，图②中，阴影部分的边长为
=2
；设小矩形的长为a，宽为b，依据等量关系即可得到方程组，进而得出a，b的值，即可得到图③中，阴影部分的面积．
【解答】解：由图可得，图①中阴影部分的边长为=2，图②中，阴影部分的边长为=2；
设小矩形的长为a，宽为b，
依题意得：
，
解得
，
∴图③中，阴影部分的面积为（a﹣3b）2=（4﹣2﹣6+6）2=44﹣16，
故答案为：44﹣16．
-
科目： 来源： 题型：
查看答案和解析>>【题目】知识背景
当a＞0且x＞0时，因为（
﹣
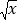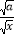）2≥0，所以x﹣2
+
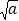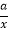≥0，从而x+
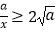（当x=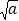时取等号）．设函数y=x+
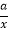（a＞0，x＞0），由上述结论可知：当x=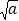时，该函数有最小值为2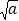．应用举例
已知函数为y1=x（x＞0）与函数y2=
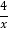（x＞0），则当x=
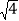=2时，y1+y2=x+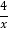有最小值为2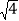=4．解决问题
（1）已知函数为y1=x+3（x＞﹣3）与函数y2=（x+3）2+9（x＞﹣3），当x取何值时，
有最小值？最小值是多少？（2）已知某设备租赁使用成本包含以下三部分：一是设备的安装调试费用，共490元；二是设备的租赁使用费用，每天200元；三是设备的折旧费用，它与使用天数的平方成正比，比例系数为0.001．若设该设备的租赁使用天数为x天，则当x取何值时，该设备平均每天的租货使用成本最低？最低是多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，等腰△ABC中，AB=AC，∠ACB=72°，
（1）若BD⊥AC于D，求∠ABD的度数；
（2）若CE平分∠ACB，求证：AE=BC．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线y=ax2+bx+c（a≠0）经过点A（3，0），B（﹣1，0），C（0，﹣3）．
（1）求该抛物线的解析式；
（2）若以点A为圆心的圆与直线BC相切于点M，求切点M的坐标；
（3）若点Q在x轴上，点P在抛物线上，是否存在以点B，C，Q，P为顶点的四边形是平行四边形？若存在，求点P的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】有一个边长为 1 的正方形，经过一次“生长”后，在他的左右肩上生出两个小正方形， 其中，三个正方形围成的三角形是直角三角形，再经过一次“生长”后，变成了下图，如果继续“生长”下去，它将变得“枝繁叶茂”，请你算出“生长”了 2019 次后形成的图形中所有的正方形的面积和是_____.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在等腰△ABC中，AB=BC=4，把△ABC沿AC翻折得到△ADC．则
（1）四边形ABCD是 形；
（2）若∠B=120°，点P、E、F分别为线段AC、AD、DC上的任意1点，则PE+PF的最小值为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在“首届中国西部（银川）房车生活文化节”期间，某汽车经销商推出A、B、C、D四种型号的小轿车共1000辆进行展销．C型号轿车销售的成交率为50%，其它型号轿车的销售情况绘制在图1和图2两幅尚不完整的统计图中．
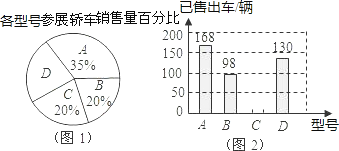
（1）参加展销的D型号轿车有多少辆？
（2）请你将图2的统计图补充完整；
（3）通过计算说明，哪一种型号的轿车销售情况最好？
（4）若对已售出轿车进行抽奖，现将已售出A、B、C、D四种型号轿车的发票（一车一票）放到一起，从中随机抽取一张，求抽到A型号轿车发票的概率．
相关试题
