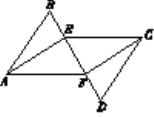
【题目】如图,AB∥CD,AB=CD,点B、E、F、D在同一条直线上,∠BAE=∠DCF.
(1)求证:AE=CF;
(2)连结AF、EC,试猜想四边形AECF是什么四边形,并证明你的结论.
参考答案:
【答案】(1)证明见解析(2)四边形AECF是平行四边形
【解析】
(1)要证AE=CF,可证△ABE≌△CDF.由AB∥CD,可知∠B=∠D,由AB=CD,已知∠BAE=∠DCF,即可证得.
(2)由△ABE≌△CDF得AE=CF,∠AEB=∠CFD,故180°-∠AEB=180°-∠CFD,即∠AEF=∠CFE,AE∥CF,AE=CF,故四边形AECF是平行四边形.
(1)证明:∵AB∥CD,∴∠B=∠D.
在△ABE和△CDF中,
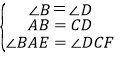 ,
,
∴△ABE≌△CDF,
∴AE=CF.
(2)四边形AECF是平行四边形.
证明:由(1)△ABE≌△CDF得AE=CF,∠AEB=∠CFD,
∴180°-∠AEB=180°-∠CFD,
即∠AEF=∠CFE.
∴AE∥CF.
又∵AE=CF,
∴四边形AECF是平行四边形.
故答案为:(1)证明见解析(2)四边形AECF是平行四边形.
-
科目: 来源: 题型:
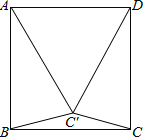
查看答案和解析>>【题目】如图,已知正方形ABCD,把边DC绕D点顺时针旋转30°到DC′处,连接AC′,BC′,CC′,写出图中所有的等腰三角形,并写出推理过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个图形中,是轴对称图形,但不是中心对称图形的是( )
A.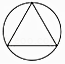
B.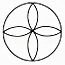
C.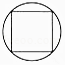
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,E,F,C在一条直线上,若将△DEC的边EC沿AC方向平移,平移过程中始终满足下列条件:AE=CF,DE⊥AC于点E,BF⊥AC于点F,且AB=CD.则当点E,F不重合时,BD与EF的关系是______.
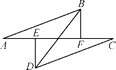
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. 直角三角形
直角三角形
B. 正五边形
正五边形
C. 正方形
正方形
D. 平行四边形
平行四边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,是轴对称图形,不是中心对称图形的是( )
A.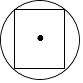
B.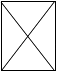
C.
D.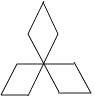
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只)
售价(元/只)
甲种节能灯
30
40
甲种节能灯
35
50
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?
相关试题

