搜索
【题目】如图所示，在Rt△ABC中，∠C=90°，∠A=30°，AB边中点D到BC边距离为3 cm，现在AC边找点E，使BE+ED值最小，则BE+ED的最小值是________cm.
参考答案：
【答案】6
【解析】
将30°的Rt△ABC补成等边三角形
,知点B和点
关于AC对称．连接D交AC于点E，则E即是所求作的点，且BE+ED的最小值即是DE的长．
解：如图：作点B关于AC对称点，DF⊥BC,连接A,D. ，则
的长为BE+ED的最小值
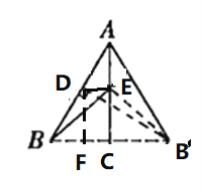
在Rt△ABC中，∠ACB=90°，AB边中点D到BC边距离为3 cm，DF⊥BC
∴DF=3，∠DFB=∠ACB=90°
∴DF//AC
∵D为AB边中点，DF//AC
∴AC=2DF=6
∵点B、点关于AC对称, ∠BAC=30°
∴
, 
∴
∴
是等边三角形
∴
又∵
∴
=6
∴BE+ED的最小值即是DE的长为:6．
故答案为:6
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E，交AC于F，过点G作GD⊥AC于D，下列四个结论：① EF=BE+CF；②∠BGC=90°+
∠A；③点G到△ABC各边的距离相等；④设GD=m，AE+AF=n,则
=mn. 其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法正确的是（ ）
A. 了解“孝感市初中生每天课外阅读书籍时间的情况”最适合的调查方式是全面调查
B. 甲乙两人跳绳各10次，其成绩的平均数相等，
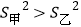，则甲的成绩比乙稳定C. 三张分别画有菱形，等边三角形，圆的卡片，从中随机抽取一张，恰好抽到中心对称图形卡片的概率是
D. “任意画一个三角形，其内角和是
”这一事件是不可能事件 -
科目： 来源： 题型：
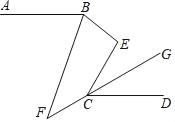
查看答案和解析>>【题目】如图，AB∥CD，∠DCE的角平分线CG的反向延长线和∠ABE的角平分线BF交于点F，∠E﹣∠F=33°，则∠E=_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知如图，△ABC在平面直角坐标系XOY中，其中A（1，2），B（3，1），C（4，3），试解答下列各题：
（1）作出△ABC关于x轴对称的△A1B1C1，并写出△A1B1C1三个顶点的坐标；A1（________）；B1（________）；C1（________）．
（2）作出△ABC关于直线a对称的△A2B2C2，并写出△A2B2C2三个顶点的坐标；A2（________）；B2（________）；C2（________）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于一个函数，如果它的自变量 x 与函数值 y 满足：当1≤x≤1 时，1≤y≤1，则称这个函数为“闭 函数”.例如：y=x，y=x 均是“闭函数”. 已知 y ax2 bx c(a0) 是“闭函数”，且抛物线经过点 A(1，1)和点 B(1，1)，则 a 的取值范围是______________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，AB=AC，∠A=36°，AC的垂直平分线交AB于E，D为垂足，连结EC．
（1）求∠ECD的度数.
（2）若CE=9，求BC的长.
相关试题
