[题目]如图.△ABC中.AB=AC.∠A=36°.AC的垂直平分线交AB于E.D为垂足.连结EC． (1)求∠ECD的度数. (2)若CE=9.求BC的长. 题目和参考答案 ——青夏教育精英家教网—

【题目】如图，△ABC中，AB=AC，∠A=36°，AC的垂直平分线交AB于E，D为垂足，连结EC．

（1）求∠ECD的度数.

（2）若CE=9，求BC的长.

参考答案：

【答案】（1）36°（2）9

【解析】

（1）根据线段垂直平分线上的点到线段两端点的距离相等可得AE=CE，然后根据等边对等角可得∠ECD=∠A；

（2）根据等腰三角形性质和三角形内角和定理求出∠B=∠ACB=72°，求出∠BEC=∠B，推出BC=CE即可．

解：（1）∵ED垂直平分AC，
∴AE=CE，
∴∠ECD=∠A，
∵∠A=36°，
∴∠ECD=36°；

（2）∵AB=AC，∠A=36°，

∴∠B=∠ACB=72°，

∵∠ECD=36°，

∴∠BCE=∠ACB-∠ECD=36°，

∠BEC=72°=∠B，

∴BC=EC=9．

相关试题

科目： 来源： 题型：

【题目】如图所示，在Rt△ABC中，∠C=90°，∠A=30°，AB边中点D到BC边距离为3 cm，现在AC边找点E，使BE+ED值最小，则BE+ED的最小值是________cm.
查看答案和解析>>
科目： 来源： 题型：

【题目】已知如图，△ABC在平面直角坐标系XOY中，其中A（1，2），B（3，1），C（4，3），试解答下列各题：
（1）作出△ABC关于x轴对称的△A1B1C1，并写出△A1B1C1三个顶点的坐标；A1（________）；B1（________）；C1（________）．
（2）作出△ABC关于直线a对称的△A2B2C2，并写出△A2B2C2三个顶点的坐标；A2（________）；B2（________）；C2（________）．
查看答案和解析>>
科目： 来源： 题型：

【题目】对于一个函数，如果它的自变量 x 与函数值 y 满足：当1≤x≤1 时，1≤y≤1，则称这个函数为“闭函数”.例如：y=x，y=x 均是“闭函数”. 已知 y ax2 bx c(a0) 是“闭函数”，且抛物线经过点 A(1，1)和点 B(1，1)，则 a 的取值范围是______________.
查看答案和解析>>
科目： 来源： 题型：

【题目】如图，在平行四边形ABCD中，E，F分别是AB，CD的中点，AF与DE相交于点G，BF与CE相交于点H．
（1）求证：四边形EHFG是平行四边形；
（2）①若四边形EHFG是菱形，则平行四边形ABCD必须满足条件　　；
②若四边形EHFG是矩形，则平行四边形ABCD必须满足条件　　．
查看答案和解析>>
科目： 来源： 题型：

【题目】海南建省30年来，各项事业取得令人瞩目的成就，以2016年为例，全省社会固定资产总投资约3730亿元，其中包括中央项目、省属项目、地（市）属项目、县（市）属项目和其他项目．图1、图2分别是这五个项目的投资额不完整的条形统计图和扇形统计图，请完成下列问题：
（1）在图1中，先计算地（市）属项目投资额为　　亿元，然后将条形统计图补充完整；
（2）在图2中，县（市）属项目部分所占百分比为m%、对应的圆心角为β，则m=　　，β=　　度（m、β均取整数）．
查看答案和解析>>
科目： 来源： 题型：

【题目】如图，已知点A（1，a）是反比例函数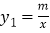的图象上一点，直线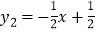与反比例函数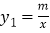的图象的交点为点B、D，且B（3，﹣1），求：
（1）求反比例函数的解析式；
（2）求点D坐标，并直接写出y1＞y2时x的取值范围；
（3）动点P（x，0）在x轴的正半轴上运动，当线段PA与线段PB之差达到最大时，求点P的坐标．
查看答案和解析>>