【题目】如图所示,矩形OABC的邻边OA、OC分别与x、y轴重合,矩形OABC的对称中心P(4,3),点Q由O向A以每秒1个单位速度运动,点M由C向B以每秒2个单位速度运动,点N由B向C以每秒2个单位速度运动,设运动时间为t秒,三点同时出发,当一点到达终点时同时停止.
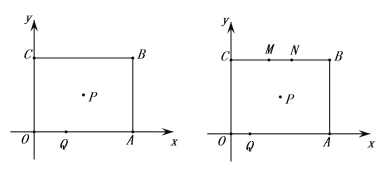
(1)根据题意,可得点B坐标为__________,AC=_________;
(2)求点Q运动几秒时,△PCQ周长最小?
(3)在点M、N、Q的运动过程中,能否使以点O、Q、M、N为顶点的四边形是平行四边形?若能,请求出t值;若不能,请说明理由.
参考答案:
【答案】(1)10 (2)![]() (3)
(3)![]() 或
或![]()
【解析】
(1)根据四边形OABC为矩形,矩形OABC的对称中心P(4,3),即可得到B的坐标,再结合勾股定理可得AC的长.
(2)首先根据题意可得△PCQ周长等于CP、CQ、PQ的线段之和,而CP是定值,进而只要CQ和PQ的和最小即可.
(3)假设能,设出t值,利用MN=OQ,计算出t值即可.
(1)根据四边形OABC为矩形,矩形OABC的对称中心P(4,3)
可得B点的坐标为(8,6)
根据勾股定理可得![]()
(2)设点Q运动t秒时,△PCQ周长最小
根据题意可得![]()
![]()
要使△PCQ周长最小,则必须CQ+PQ最短,过x轴作P点的对称点P’

所以可得C、P’、Q在一条直线上
![]() C(0,6),
C(0,6),![]() (4,-3)
(4,-3)
设直线方程为![]()
![]() 即
即
因此![]() ,C所在的直线为
,C所在的直线为![]()
所以Q点的坐标为(![]() ,0)
,0)
所以OQ=![]()
因此t=![]()
(3)根据题意要使点O、Q、M、N为顶点的四边形是平行四边形
则OQ=MN
OQ=t
MN=8-2t-2t=8-4t或MN=2t+2t-8=4t-8
所以t=8-4t或t=4t-8
所以可得t=![]() 或t=
或t=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AB的中点,连接DE、CE.
(1)求证:△ADE≌△BCE;
(2)若AB=6,AD=4,求△CDE的周长.

-
科目: 来源: 题型:
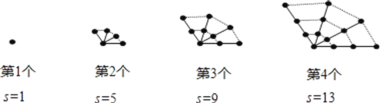
查看答案和解析>>【题目】观察图中给出的四个点阵,s表示每个点阵中的点的个数,按照图形中的点的个数变化规律,猜想第10个点阵中的点的个数s为( ).
A.
 B.
B. C.
C.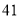 D.
D.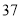
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )

A. 4:2:1 B. 5:3:1 C. 25:12:5 D. 51:24:10
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=
 在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=10,则k的值是( )
在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=10,则k的值是( )
A. 3 B. 4 C. 5 D. 4

-
科目: 来源: 题型:
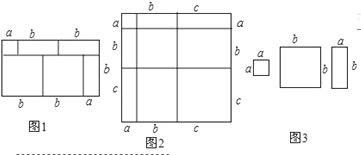
查看答案和解析>>【题目】阅读下列文字:
我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如由图1可以得到(a+2b)(a+b)=a2+3ab+2b2.请解答下列问题:
(1)写出图2中所表示的数学等式_____;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)图3中给出了若干个边长为a和边长为b的小正方形纸片及若干个边长分别为a、b的长方形纸片,
①请按要求利用所给的纸片拼出一个几何图形,并画在图3所给的方框中,要求所拼出的几何图形的面积为2a2+5ab+2b2,
②再利用另一种计算面积的方法,可将多项式2a2+5ab+2b2分解因式.即2a2+5ab+2b2=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于_____.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923101670465536/1923902127538176/STEM/3534c7f6f1a5489684ae6308493b71da.png]
相关试题

