【题目】如图1所示,已知函数y=![]() (x>0)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0).动点M是y轴正半轴上点B上方的点.动点N在射线AP上,过点B作AB的垂线,交射线AP于点D.交直线MN于点Q.连接AQ.取AQ的中点C.
(x>0)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0).动点M是y轴正半轴上点B上方的点.动点N在射线AP上,过点B作AB的垂线,交射线AP于点D.交直线MN于点Q.连接AQ.取AQ的中点C.
(1)如图2,连接BP,求△PAB的面积;
(2)当点Q在线段BD上时,若四边形BQNC是菱形,面积为2![]() ,求此时P点的坐标;
,求此时P点的坐标;
(3)在(2)的条件下,在平面直角坐标系中是否存在点S,使得以点D、Q、N、S为项点的四边形为平行四边形?如果存在,请直接写出所有的点S的坐标;如果不存在,请说明理由.

参考答案:
【答案】(1)3;(2)P(3,2);(3) 点S的坐标为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)首先连接OP,可得![]() ;
;
(2)由四边形BQNC是菱形,![]() ,C是AQ的中点,易求得
,C是AQ的中点,易求得![]() ,继而可得
,继而可得![]() ,然后设
,然后设![]() ,求得
,求得![]() 的值,继而可求得答案;
的值,继而可求得答案;
(3)首先由(2),求得点D、Q、N的坐标,然后分别从QD、DN、QN为对角线去分析求解即可求得答案.
(1)连接OP,

则![]() ;
;
(2)∵四边形BQNC是菱形,
![]() ,
,![]() ,
,
![]() ,C是AQ的中点,
,C是AQ的中点,
![]() ,
,
![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
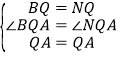 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∵![]() ,
,
设![]() ,
,
则![]() ,
,
解得![]() ,即
,即![]() ,
,
∵在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
又∵P点在函数![]() 的图像上,
的图像上,
∴P点坐标为![]() ;
;
(3)∵在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
∴在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() 的坐标为
的坐标为![]() ,N的坐标为
,N的坐标为![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
∴点D的坐标为![]() ,
,
∴若四边形QNDS是平行四边形,则![]() ,
,![]() ,则点S的坐标为
,则点S的坐标为![]() ,
,
若四边形QNSD是平行四边形,则![]() ,
,![]() ,则点S的坐标为
,则点S的坐标为![]() ,
,
若四边形QNDS是平行四边形,则![]() ,
,![]() ,则点S的坐标为
,则点S的坐标为![]() ,
,
综上所述,点S的坐标为![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ABC=∠ADC=90°,AB=AD,E是AC的中点.
(1)求证:∠EBD=∠EDB
(2)若∠BED=120°,试判断△BDC的形状.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=kx+b的图象与反比例函数
 的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是﹣2,
的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是﹣2,求:(1)一次函数的解析式;
(2)△AOB的面积;
(3)直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=-
 x+8与x轴交于A点,与y轴交于B点,动点P从A点出发,以每秒2个单位的速度沿AO方向向点O匀速运动,同时动点Q从B点出发,以每秒1个单位的速度沿BA方向向点A匀速运动,当一个点停止运动,另一个点也随之停止运动,连接PQ,设运动时间为t(s)(0<t≤3).
x+8与x轴交于A点,与y轴交于B点,动点P从A点出发,以每秒2个单位的速度沿AO方向向点O匀速运动,同时动点Q从B点出发,以每秒1个单位的速度沿BA方向向点A匀速运动,当一个点停止运动,另一个点也随之停止运动,连接PQ,设运动时间为t(s)(0<t≤3).(1)写出A,B两点的坐标;
(2)当t为何值时,以点A,P,Q为顶点的三角形与△ABO相似,并直接写出此时点Q的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,分别以△ABC的边AB、AC为一边向形外作正方形ABDE和正方形ACGF.求证S△AEF=S△ABC.
(2)如图②,分别以△ABC的边AB、AC、BC为边向形外作正方形ABDE、ACGF、BCHI,可得六边形DEFGHI,若S正方形ABDE=17,S正方形ACGF=25,S正方形BCHI=16,求S六边形DEFGHI.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“面积法”是指利用图形面积间的等量关系寻求线段间等量关系的一种方法.例如:在△ABC中,AB=AC,点P是BC所在直线上一个动点,过P点作PD⊥AB、PE⊥AC,垂足分别为D、E,BF为腰AC上的高.如图①,当点P在边BC上时,我们可得如下推理:
∵S△ABC=S△ABP+S△ACP
∴
 ACBF=
ACBF= ABPD+
ABPD+ ACPE
ACPE∵AB=AC
∴
 ACBF=
ACBF= AC(PD+PE)
AC(PD+PE)∴BF=PD+PE

(1)(变式)如图②,在上例的条件下,当点P运动到BC的延长线上时,试探究BF、PD、PE之间的关系,并说明理由.
(2)(迁移)如图③,点P是等边△ABC内部一点,作PD⊥AB、PE⊥BC、PF⊥AC,垂足分别为D、E、F,若PD=1,PE=2,PF=4.求△ABC的边长.
(3)(拓展)若点P是等边△ABC所在平面内一点,且点P到三边所在直线的距离分别为2、3、6.请直接写出等边△ABC的高的所有可能
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△BAD中,AD交BC于点O,∠1=∠2,添加下列条件仍不能判定△ABC≌△BAD的是( )

A.∠C=∠DB.AD=BCC.∠3=∠4D.AC=BD
相关试题

