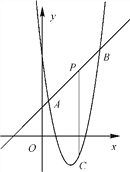
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6相交于A(![]() ,
, ![]() )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴,交抛物线于点C.
(1)求抛物线的表达式;
(2)是否存在这样的点P,使线段PC的长有最大值?若存在,求出这个最大值,若不存在,请说明理由;
(3)当△PAC为直角三角形时,求点P的坐标.
参考答案:
【答案】(1)y=2x2-8x+6(2)存在符合条件的点P(![]() ,
, ![]() ),使线段PC的长有最大值
),使线段PC的长有最大值![]() .(3)满足条件的点P有两个,为P1(3,5),P2(
.(3)满足条件的点P有两个,为P1(3,5),P2(![]() ,
, ![]() ).
).
【解析】试题分析:(1)通过直线AB的解析式求出B点坐标。将点A和点B的坐标代入抛物线的解析式中得到一组关于a、b的二元一次方程组,解方程组求出a、b的值并代回抛物线的解析式中即可。
(2)根据直线AB的解析式设出点P的坐标。点P与点C的横坐标相同,由抛物线的解析式得出点C的坐标,即可得出PC关于点P坐标的表达式。根据二次函数的性质求出PC的长的最大值,即可求出点P的坐标。
(3)当△PAC是直角三角形时,有①∠PAC=90°和②∠PCA=90°这两种情况,分别求出这两种情况下的点P的坐标即可。
解:(1)∵B(4,m)在直线y=x+2上,
∴m=6,B(4,6).
∵A(![]() ,
,![]() )、B(4,6)在抛物线y=ax2+bx+6上,
)、B(4,6)在抛物线y=ax2+bx+6上,
∴ 解得
解得![]()
∴所求抛物线的表达式为y=2x2-8x+6.
(2)设动点P的坐标为(n,n+2),则点C的坐标为(n,2n2-8n+6).
∴PC=(n+2)-(2n2-8n+6)=-2n2+9n-4=-2(n-![]() )2+
)2+![]() .∵a=-2<0,
.∵a=-2<0,
∴当n=![]() 时,线段PC取得最大值
时,线段PC取得最大值![]() ,此时,P(
,此时,P(![]() ,
,![]() ).
).
综上所述,存在符合条件的点P(![]() ,
,![]() ),使线段PC的长有最大值
),使线段PC的长有最大值![]() .
.
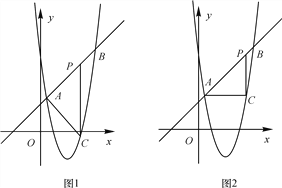
(3)显然,∠APC≠90°,如图1,当∠PAC=90°时,设直线AC的表达式为y=-x+b,把A(![]() ,
,![]() )代入,得-
)代入,得-![]() +b=
+b=![]() .解得b=3.由-x+3=2x2-8x+6,得x1=3或x2=
.解得b=3.由-x+3=2x2-8x+6,得x1=3或x2=![]() (舍去).
(舍去).
当x=3时,x+2=3+2=5.此时,点P的坐标为P1(3,5).
如图2,当∠PCA=90°时,由A(![]() ,
,![]() )知,点C的纵坐标为y=
)知,点C的纵坐标为y=![]() .
.
由2x2-8x+6=![]() ,得x1=
,得x1=![]() (舍去),x2=
(舍去),x2=![]() .当x=
.当x=![]() 时,x+2=
时,x+2=![]() +2=
+2=![]() .
.
此时,点P的坐标为P2(![]() ,
,![]() ).
).
综上可知,满足条件的点P有两个,为P1(3,5),P2(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个加工厂计划为某开发公司加工一批产品,已知甲、乙两个工厂每天分别能加工这种产品16件和24件,且单独加工这批产品甲厂比乙厂要多用20天,已知由甲厂单独做,公司需付甲厂每天费用180元;若由乙厂单独做,公司需付乙厂每天费用220元.
(1)求加工的这批产品共有多少件?
(2)若由一个加工厂单独加工完成,选用哪个加工厂费用较低?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在平面直角坐标系xOy中,点A(-4,0),点B在直线y=x+2上.当A、B两点间的距离最小时,点B的坐标是( )
A. (
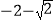 ,
,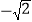 ) B. (
) B. (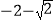 ,
,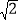 ) C. (-3,-1) D. (-3,
) C. (-3,-1) D. (-3,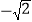 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N.
(1)当∠MAN绕点A旋转到BM=DN时(如图1),请你直接写出BM、DN和MN的数量关系:__________.
(2)当∠MAN绕点A旋转到BM≠DN时(如图2),(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)当∠MAN绕点A旋转到如图3的位置时,线段BM、DN和MN之间又有怎样的数量关系?请写出直接写出结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在关系式
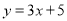 中有下列说法:①x是自变量,y是因变量;②x的数值可以任意选择;③y是变量,它的值与x无关;④用关系式表示的不能用图像表示;⑤y与x的关系还可以用列表法和图像法表示,其中说法正确的是( ).
中有下列说法:①x是自变量,y是因变量;②x的数值可以任意选择;③y是变量,它的值与x无关;④用关系式表示的不能用图像表示;⑤y与x的关系还可以用列表法和图像法表示,其中说法正确的是( ).A.①②⑤B.①②④C.①③⑤D.①④⑤
-
科目: 来源: 题型:
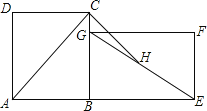
查看答案和解析>>【题目】如图,在长方形ABCD中,AC是对角线.将长方形ABCD绕点B顺时针旋转90°到长方形GBEF位置,H是EG的中点.若AB=6,BC=8,则线段CH的长为( )
A.
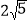 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】将函数 y=2x+b(b为常数)的图象位于x轴下方的部分沿x轴翻折至其上方,所得的折线是函数y=
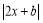 (b为常数)的图象,若该图象在直线y=1下方的点的横坐标x满足0<x<3,则 b的取值范围为( )
(b为常数)的图象,若该图象在直线y=1下方的点的横坐标x满足0<x<3,则 b的取值范围为( )A.-5≤b≤-1B.-3≤b≤-1C.-2≤b≤0D.-3≤b≤0
相关试题

