【题目】将函数 y=2x+b(b为常数)的图象位于x轴下方的部分沿x轴翻折至其上方,所得的折线是函数y=![]() (b为常数)的图象,若该图象在直线y=1下方的点的横坐标x满足0<x<3,则 b的取值范围为( )
(b为常数)的图象,若该图象在直线y=1下方的点的横坐标x满足0<x<3,则 b的取值范围为( )
A.-5≤b≤-1B.-3≤b≤-1C.-2≤b≤0D.-3≤b≤0
参考答案:
【答案】A
【解析】
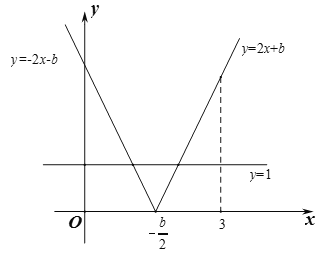
根据题意,直线y=2x+b的图象沿x轴翻折后的函数关系式是y=-2x-b,如图,两函数与x轴的交点坐标为(![]() ,0),且对y=-2x-b,当x=0时y=-b≥1;对y=2x+b,当x=3时,y=6+b≥1;据此列出不等式组,再求解即可.
,0),且对y=-2x-b,当x=0时y=-b≥1;对y=2x+b,当x=3时,y=6+b≥1;据此列出不等式组,再求解即可.
解:如图,根据题意,直线y=2x+b的图象沿x轴翻折后的函数关系式是y=-2x-b,两函数与x轴的交点坐标为(![]() ,0),且对y=-2x-b,当x=0时y=-b≥1;对y=2x+b,当x=3时,y=6+b≥1;可列出不等式组
,0),且对y=-2x-b,当x=0时y=-b≥1;对y=2x+b,当x=3时,y=6+b≥1;可列出不等式组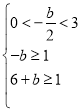 ,解得-5≤b≤-1.
,解得-5≤b≤-1.
故选A.
-
科目: 来源: 题型:
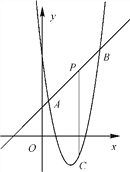
查看答案和解析>>【题目】如图,直线y=x+2与抛物线y=ax2+bx+6相交于A(
 ,
, 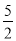 )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴,交抛物线于点C.(1)求抛物线的表达式;
(2)是否存在这样的点P,使线段PC的长有最大值?若存在,求出这个最大值,若不存在,请说明理由;
(3)当△PAC为直角三角形时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在关系式
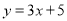 中有下列说法:①x是自变量,y是因变量;②x的数值可以任意选择;③y是变量,它的值与x无关;④用关系式表示的不能用图像表示;⑤y与x的关系还可以用列表法和图像法表示,其中说法正确的是( ).
中有下列说法:①x是自变量,y是因变量;②x的数值可以任意选择;③y是变量,它的值与x无关;④用关系式表示的不能用图像表示;⑤y与x的关系还可以用列表法和图像法表示,其中说法正确的是( ).A.①②⑤B.①②④C.①③⑤D.①④⑤
-
科目: 来源: 题型:
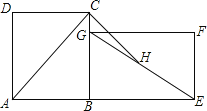
查看答案和解析>>【题目】如图,在长方形ABCD中,AC是对角线.将长方形ABCD绕点B顺时针旋转90°到长方形GBEF位置,H是EG的中点.若AB=6,BC=8,则线段CH的长为( )
A.
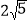 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能的是( )

A. 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B. 一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C. 暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
D. 掷一个质地均匀的正六面体骰子,向上的面点数是4
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据研究,人体内血乳酸浓度升高是运动后感觉疲劳的重要原因,运动员未运动时,体内血乳酸浓度水平通常在40mg/L以下;如果血乳酸浓度降到50mg/L以下,运动员就基本消除了疲劳,体育科研工作者根据实验数据,绘制了一副图象,它反映了运动员进行高强度运动后,体内血乳酸浓度随时间变化而变化的函数关系.
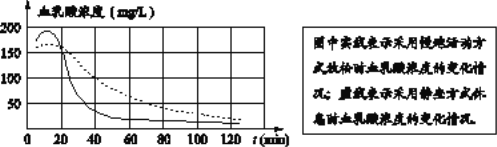
下列叙述正确的是
A. 运动后40min时,采用慢跑活动方式放松时的血乳酸浓度与采用静坐方式休息时的血乳酸浓度相同
B. 运动员高强度运动后最高血乳酸浓度大约为350mg/L
C. 运动员进行完剧烈运动,为了更快达到消除疲劳的效果,应该采用慢跑活动方式来放松
D. 采用慢跑活动方式放松时,运动员必须慢跑80min后才能基本消除疲劳
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接CF.
(1)求证:四边形ABDF是平行四边形;
(2)若∠CAF=45°,BC=4,CF=
 ,求△CAF的面积.
,求△CAF的面积.
相关试题

