搜索
【题目】如图，在△ABC中，∠ABC = 90°，AB = 7，AC = 25，BC = 24，三条角平分线相交相交于点P，求点P到AB的距离．
参考答案：
【答案】3.
【解析】试题分析：
用两种方式表示△ABC的面积，S△ABC=
AB×BC；因为点P是三条角平分线的交点，所以点P到三角形的三边的距离相等，设点P到三边的距离为h，则S△ABC=S△ABP+S△BCP+S△ACP，列方程求解.
试题解析：
∵∠ABC=90°，∴S△ABC=AB×BC=×7×24=84.
∵三条角平分线相交相交于点P，∴点P到三角形的三边的距离相等.
设点P到三边的距离为h，
则S△ABC=S△ABP+S△BCP+S△ACP
=h×AB+h×BC+h×AC
=h（AB+BC+AC）=h（7+24+25）=28h.
∴28h=84，解得h=3.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为（－3，2），（－1，3），（2，1）．
（1）作出与△ABC关于x轴对称的△A1B1C1（点A，B，C的对应点分别是A1，B1，C1）；
（2）连接AA1，CC1，求出四边形AA1 C1C的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某人按定期2年向银行储蓄，若年利率为3％（不计复利），到期支取时他活的利息为90元，则他存入的本金为（ ）
A. 3000 B. 2500 C. 1500 D. 1000
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y=kx+b（k≠0）的图象过点P（﹣
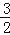，0），且与反比例函数y=
（m≠0）的图象相交于点A（﹣2，1）和点B． （1）求一次函数和反比例函数的解析式；
（2）求点B的坐标，并根据图象回答：当x在什么范围内取值时，一次函数的函数值小于反比例函数的函数值？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，AB的垂直平分线交AB于M，交AC于N．
（1）若∠ABC=70°，则∠MNA的度数是__．
（2）连接NB，若AB=8cm，△NBC的周长是14cm．
①求BC的长；
②在直线MN上是否存在P，使由P、B、C构成的△PBC的周长值最小？若存在，标出点P的位置并求△PBC的周长最小值；若不存在，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】以下可以用来证明命题“任何偶数都是4的倍数”是假命题的反例为（ ）
A. 3 B. 4 C. 8 D. 6
-
科目： 来源： 题型：
查看答案和解析>>【题目】课本中有一道作业题：
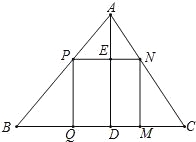
有一块三角形余料ABC，它的边BC=120mm，高AD=80mm．要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB，AC上．问加工成的正方形零件的边长是多少mm？
小颖解得此题的答案为48mm，小颖善于反思，她又提出了如下的问题：
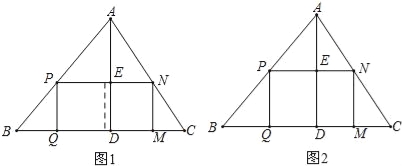
（1）如果原题中要加工的零件是一个矩形，且此矩形是由两个并排放置的正方形所组成，如图1，此时，这个矩形零件的两条边长又分别为多少mm？请你计算．
（2）如果原题中所要加工的零件只是一个矩形，如图2，这样，此矩形零件的两条边长就不能确定，但这个矩形面积有最大值，求达到这个最大值时矩形零件的两条边长．
相关试题
