【题目】如图，一次函数y=kx+b（k≠0）的图象过点P（﹣，0），且与反比例函数y=（m≠0）的图象相交于点A（﹣2，1）和点B．

（1）求一次函数和反比例函数的解析式；

（2）求点B的坐标，并根据图象回答：当x在什么范围内取值时，一次函数的函数值小于反比例函数的函数值？

参考答案：

【答案】(1)、y=；y=-2x-3；(2)、＜x＜0或x>.

【解析】

试题分析：(1)、将点A代入求出反比例函数解析式；将点P和点A代入函数解析式求出答案；(2)、首先求出函数的交点，然后根据图像得出答案.

试题解析：(1)、∵ 反比例函数y= （m≠0）的图象经过点A（﹣2，1） ∴=1 解得m=-2

∵一次函数y=kx+b（k≠0）的图象过点P（－，0）和A（﹣2，1）

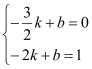∴ 解得：

∴反比例函数的解析式是y= 一次函数的解析式是y=-2x-3

(2)、、联立方程组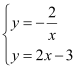： 解得：

∴ B点坐标是（ ，-4）

当＜x＜0或x> 时，一次函数的函数值小于反比例函数的函数值

关闭