【题目】如图,数轴上有点a,b,c三点
![]()
(1)用“<”将a,b,c连接起来.
(2)b﹣a 1(填“<”“>”,“=”)
(3)化简|c﹣b|﹣|c﹣a+1|+|a﹣1|
(4)用含a,b的式子表示下列的最小值:
①|x﹣a|+|x﹣b|的最小值为 ;
②|x﹣a|+|x﹣b|+|x+1|的最小值为 ;
③|x﹣a|+|x﹣b|+|x﹣c|的最小值为 .
参考答案:
【答案】(1) b>a>c;(2) <;(3)b;(4)①b﹣a;②b+1;③b-c.
【解析】
(1)比较有理数的大小可以利用数轴,它们从左到右的顺序,即从小到大的顺序(在数轴上表示的两个有理数,右边的数总比左边的数大);
(2)先求出b-a的范围,再比较大小即可求解;
(3)先计算绝对值,再合并同类项即可求解;
(4)根据绝对值的性质以及题意即可求出答案.
(1)根据数轴上的点得:b>a>c;
(2)由题意得:b-a<1;
(3)|c-b|-|c-a+1|+|a-1|
=b-c-(a-c-1)+a-1
=b-c-a+c+1+a-1
=b;
(4)①当x在a和b之间时,|x-a|+|x-b|有最小值,
∴|x-a|+|x-b|的最小值为:x-a+b-x=b-a;
②当x=a时,
|x-a|+|x-b|+|x+1|=0+b-x+x-(-1)=b+1为最小值;
③当x=a时,
|x-a|+|x-b|+|x-c|=0+b-a+a-c=b-c为最小值.
故答案为:<;b-a;b+1;b-c.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAC和∠DAE都是70°30′的角.
(1)如果∠DAC=27°30′,那么∠BAE等于多少度?(写出过程)
(2)请写出图中相等的角;
(3)若∠DAC变大,则∠BAD如何变化?

-
科目: 来源: 题型:
查看答案和解析>>【题目】规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.当﹣1<x<1时,化简 [x]+(x)+[x)的结果是__________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)画出数轴,并在数轴上画出表示下列各数的点:﹣4.5,﹣2,3,0,4;
(2)用“<”号将(1)中各数连接起来;
(3)直接填空:数轴上表示3和表示1的两点之间的距离是_____,数轴上A点表示的数为4,B点表示的数为﹣2,则A、B之间的距离是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列单项式的排列规律:3x,
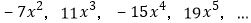 ,照这样排列第10个单项式应是
,照这样排列第10个单项式应是
A. 39x10 B. -39 x10 C. -43 x10 D. 43 x10
-
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读)|4﹣1|表示4与1差的绝对值,也可以理解为4与1两数在数轴上所对应的两点之间的距离;|4+1|可以看做|4﹣(﹣1)|,表示4与﹣1的差的绝对值,也可以理解为4与﹣1两数在数轴上所对应的两点间的距离.
(1)|4﹣(﹣1)|=
(2)|5+2|=
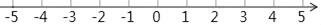
(3)利用数轴找出所有符合条件的整数x,使得|x+3|=5,则x= .
(4)利用数轴找出所有符合条件的整数x,使得|x+3|+|x﹣2|=5,这样的整数是: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果∠α和∠β互补,且∠α<∠β,下列表达式:①90°﹣∠α;②∠β﹣90°;③
 (∠β+∠α);④
(∠β+∠α);④ (∠β﹣∠α)中,等于∠α的余角的式子有( )
(∠β﹣∠α)中,等于∠α的余角的式子有( )A. 1个 B. 2个 C. 3个 D. 4个
相关试题

