搜索
【题目】动物学家通过大量的调查估计出，某种动物活到20岁的概率为0.8，活到25岁的概率是0.5，活到30岁的概率是0.3．现年20岁的这种动物活到25岁的概率为多少？现年25岁的这种动物活到30岁的概率为多少？
参考答案：
【答案】现年20岁的这种动物活到25岁的概率为0.625，现年25岁的这种动物活到30岁的概率为0.6．
【解析】试题分析：
根据概率的定义，用活到25岁的概率除以活到20岁的概率可得到现年20岁的这种动物活到25岁的概率；用活到30岁的概率除以活到25岁的概率可得到现年25岁的这种动物活到30岁的概率
试题解析：
现年20岁的这种动物活到25岁的概率为
=0.625，
现年25岁的这种动物活到30岁的概率为
=0.6，
答：现年20岁的这种动物活到25岁的概率为0.625，现年25岁的这种动物活到30岁的概率为0.6．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法正确的是（ ）
A．一个游戏的中奖概率是
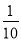，则做10次这样的游戏一定会中奖B．为了解全国中学生的心理健康情况，应该采用普查的方式
C．一组数据6，8，7，8，8，9，10的众数和中位数都是8
D．若甲组数据的方差S2甲=0．01，乙组数据的方差S2乙=0．1，则乙组数据比甲组数据稳定
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形
中，点
是
边上的一个动点，连接
．过点
作一条射线与边
的延长线交于点
，使得
，其中
是边
延长线上的点．连接
．（
）求证： 
是等腰直角三角形．（
）若
，求
的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】观察下列方程及解的特征： ⑴x+
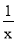=2的解为x1=x2=1；⑵x+
=
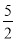的解为x1=2，x2=
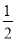；⑶x+
=
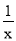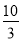的解为x1=3，x2=
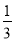； 解答下列问题：
（1）请猜想：方程x+
=
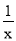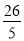的解为________； （2）请猜想：关于x的方程x+
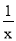═________的解为x1=a，x2=
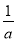（a≠0）； （3）下面以解方程x+
=
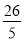为例，验证（1）中猜想结论的正确性． -
科目： 来源： 题型：
查看答案和解析>>【题目】小明和小亮玩一个游戏：三张大小、质地都相同的卡片上分别标有数字2，3，4(背面完全相同)，现将标有数字的一面朝下．小明从中任意抽取一张，记下数字后放回洗匀，然后小亮从中任意抽取一张，计算小明和小亮抽得的两个数字之和．若和为奇数，则小明胜；若和为偶数，则小亮胜．
(1)请你用画树状图或列表的方法，求出这两数和为6的概率．
(2)你认为这个游戏规则对双方公平吗？说说你的理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】有
、
、
三家工厂依次坐落在一条笔直的公路边，甲、乙两辆运货卡车分别从
、
工厂同时出发，沿公路匀速驶向
工厂，最终到达
工厂，设甲、乙两辆卡车行驶
后，与
工厂的距离分别为
、
（
）．
、
与
函数关系如图所示，根据图象解答下列问题．（提示：图中较粗的折线表示的是
与
的函数关系．）（
）
、
两家工厂之间的距离为__________ 
， 
__________， 
点坐标是__________．（
）求甲、乙两车之间的距离不超过
时， 
的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，
的角平分线BD、CE相交于点P.（1）如果
，求∠BPC的度数；（2）如图2，作
外角
的角平分线交于点Q，试探索
、
之间的数量关系。（3）如图3，延长线段BP、QC交于点E，△BQE中，存在一个内角等于另一个内角的2倍，求
的度数
相关试题
