【题目】有![]() 、
、![]() 、
、![]() 三家工厂依次坐落在一条笔直的公路边,甲、乙两辆运货卡车分别从
三家工厂依次坐落在一条笔直的公路边,甲、乙两辆运货卡车分别从![]() 、
、![]() 工厂同时出发,沿公路匀速驶向
工厂同时出发,沿公路匀速驶向![]() 工厂,最终到达
工厂,最终到达![]() 工厂,设甲、乙两辆卡车行驶
工厂,设甲、乙两辆卡车行驶![]() 后,与
后,与![]() 工厂的距离分别为
工厂的距离分别为![]() 、
、![]() (
(![]() ).
).![]() 、
、![]() 与
与![]() 函数关系如图所示,根据图象解答下列问题.(提示:图中较粗的折线表示的是
函数关系如图所示,根据图象解答下列问题.(提示:图中较粗的折线表示的是![]() 与
与![]() 的函数关系.)
的函数关系.)
(![]() )
)![]() 、
、![]() 两家工厂之间的距离为__________
两家工厂之间的距离为__________ ![]() ,
, ![]() __________,
__________, ![]() 点坐标是__________.
点坐标是__________.
(![]() )求甲、乙两车之间的距离不超过
)求甲、乙两车之间的距离不超过![]() 时,
时, ![]() 的取值范围.
的取值范围.

参考答案:
【答案】(1)见解析;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)根据y轴的最大距离为B、C两地间的距离,再加上A、B两地间的距离即可;先求出甲的速度,再求出到达C地的时间,然后加上0.5即为a的值;利用待定系数法求一次函数解析式求出甲从B地到C地的函数解析式,再求出乙的解析式,然后联立求解即可得到点P的坐标;
(2)根据两函数解析式列出不等式组求解即可.
试题解析:解:(1)由图可知,A、B两地相距30km,B、C两地相距90km,所以,A、C两家工厂之间的距离为30+90=120km,甲的速度为:30÷0.5=60km/h,90÷60=1.5小时,∴a=0.5+1.5=2;
设甲:0.5≤x≤2时的函数解析式为y=kx+b,∵函数图象经过点(0.5,0)、(2,90),∴![]() ,解得:
,解得: ![]() ,∴y=60x﹣30,乙的速度为90÷3=30km/h,乙函数解析式为:y=30x,联立
,∴y=60x﹣30,乙的速度为90÷3=30km/h,乙函数解析式为:y=30x,联立![]() ,解得:
,解得: ![]() ,所以,点P(1,30);
,所以,点P(1,30);
故答案为:120,2,(1,30);
(2)∵甲、乙两车之间的距离不超过10km,∴ ![]() ,解不等式①得,x≥
,解不等式①得,x≥![]() ,解不等式②得,x≤
,解不等式②得,x≤![]() ,所以,x的取值范围是
,所以,x的取值范围是![]() ≤x≤
≤x≤![]() ;
;
当甲车停止后,乙行驶![]() 小时时,两车相距10km,故
小时时,两车相距10km,故![]() ≤x≤3时,甲、乙两车之间的距离不超过10km.
≤x≤3时,甲、乙两车之间的距离不超过10km.
综上所述:x的取值范围是![]() ≤x≤
≤x≤![]() 或
或![]() ≤x≤3甲、乙两车之间的距离不超过10km.
≤x≤3甲、乙两车之间的距离不超过10km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列方程及解的特征: ⑴x+
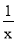 =2的解为x1=x2=1;
=2的解为x1=x2=1;⑵x+
 =
=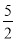 的解为x1=2,x2=
的解为x1=2,x2=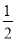 ;
;⑶x+
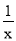 =
=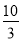 的解为x1=3,x2=
的解为x1=3,x2=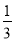 ;
; 解答下列问题:
(1)请猜想:方程x+
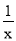 =
=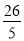 的解为________;
的解为________; (2)请猜想:关于x的方程x+
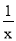 ═________的解为x1=a,x2=
═________的解为x1=a,x2=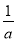 (a≠0);
(a≠0); (3)下面以解方程x+
 =
=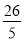 为例,验证(1)中猜想结论的正确性.
为例,验证(1)中猜想结论的正确性. -
科目: 来源: 题型:
查看答案和解析>>【题目】动物学家通过大量的调查估计出,某种动物活到20岁的概率为0.8,活到25岁的概率是0.5,活到30岁的概率是0.3.现年20岁的这种动物活到25岁的概率为多少?现年25岁的这种动物活到30岁的概率为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小亮玩一个游戏:三张大小、质地都相同的卡片上分别标有数字2,3,4(背面完全相同),现将标有数字的一面朝下.小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和.若和为奇数,则小明胜;若和为偶数,则小亮胜.
(1)请你用画树状图或列表的方法,求出这两数和为6的概率.
(2)你认为这个游戏规则对双方公平吗?说说你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
 的角平分线BD、CE相交于点P.
的角平分线BD、CE相交于点P.(1)如果
 ,求∠BPC的度数;
,求∠BPC的度数;(2)如图2,作
 外角
外角 的角平分线交于点Q,试探索
的角平分线交于点Q,试探索 、
、 之间的数量关系。
之间的数量关系。(3)如图3,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求
 的度数
的度数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD、BEFG均为正方形,连接AG、CE.
(1)求证:AG=CE;
(2)求证:AG⊥CE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC三个顶点的坐标分别为(1,2),(-2,3),(-1,0),把它们的横坐标和纵坐标都扩大到原来的2倍,得到点
 ,
,  ,
,  .下列说法正确的是( )
.下列说法正确的是( )
A. △
 与△ABC是位似图形,位似中心是点(1,0)
与△ABC是位似图形,位似中心是点(1,0)B. △
 与△ABC是位似图形,位似中心是点(0,0)
与△ABC是位似图形,位似中心是点(0,0)C. △
 与△ABC是相似图形,但不是位似图形
与△ABC是相似图形,但不是位似图形D. △
 与△ABC不是相似图形
与△ABC不是相似图形
相关试题

