【题目】如图,直线AB∥CD,AE平分∠CAB,AE与CD相交于点E,∠ACD=40°,则∠DEA=( )
A.40°
B.110°
C.70°
D.140°
参考答案:
【答案】B
【解析】解:∵AB∥CD,
∴∠ACD+∠BAC=180°,
∵∠ACD=40°,
∴∠BAC=180°﹣40°=140°,
∵AE平分∠CAB,
∴∠BAE= ![]() ∠BAC=
∠BAC= ![]() ×140°=70°,
×140°=70°,
∴∠DEA=180°﹣∠BAE=110°.
所以答案是:B.
【考点精析】解答此题的关键在于理解角的平分线的相关知识,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线,以及对平行线的性质的理解,了解两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,AB=BC=6,∠B=60°,∠D=90°,连结AC.动点P从点B出发,沿BC以每秒1个单位的速度向终点C运动(点P不与点B、C重合).过点P作PQ⊥BC交AB或AC于点Q,以PQ为斜边作Rt△PQR,使PR∥AB.设点P的运动时间为t秒.

(1)当点Q在线段AB上时,求线段PQ的长.(用含t的代数式表示)
(2)当点R落在线段AC上时,求t的值.
(3)设△PQR与△ABC重叠部分图形的面积为S平方单位,求S与t之间的函数关系式.
(4)当点R到C、D两点的距离相等时,直接写出t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD、EF被直线GH所截,已知AB//CD,∠1+∠2=180°,请填写CD//EF的理由.
解:因为∠1=∠3( )
_____________________(已知)
所以∠2+∠3=180°( )
得AB//EF( )
因为AB//CD( )
所以CD//EF( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=﹣x+3与抛物线
 交于A、B两点,点A在x轴上,点B的横坐标为
交于A、B两点,点A在x轴上,点B的横坐标为  .动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
.动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
(1)求b、c的值.
(2)当点N落在直线AB上时,直接写出m的取值范围.
(3)当点P在A、B两点之间的抛物线上运动时,设正方形PQMN的周长为C,求C与m之间的函数关系式,并写出C随m增大而增大时m的取值范围.
(4)当△PQM与坐标轴有2个公共点时,直接写出m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB//CD,分别探究下列三个图形中∠APC和∠PAB,∠PCD的关系.

结论:(1)__________________________
(2)__________________________
(3)__________________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,对角线AC与BD交于点O,若增加一个条件,使ABCD成为菱形,下列给出的条件不正确的是( )

A.AB=AD
B.AC⊥BD
C.AC=BD
D.∠BAC=∠DAC -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点
 为第一象限内一点,点
为第一象限内一点,点 为
为 轴正半轴上一点,分别连接
轴正半轴上一点,分别连接 ,
, ,
, 为等边三角形,点
为等边三角形,点 的横坐标为4.
的横坐标为4.
(1)如图1,求线段
 的长;
的长;(2)如图2,点
 在线段
在线段 上(点
上(点 不与点
不与点 、点
、点 重合),点
重合),点 在线段
在线段 的延长线上,连接
的延长线上,连接 ,
, ,
, ,设
,设 的长为
的长为 ,
, 的长为
的长为 ,求
,求 与
与 的关系式(不要求写出
的关系式(不要求写出 的取值范围)
的取值范围)(3)在(2)的条件下,点
 为第四象限内一点,分别连接
为第四象限内一点,分别连接 ,
,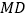 ,
, ,
, 为等边三角形,线段
为等边三角形,线段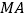 的垂直平分线交
的垂直平分线交 的延长线于点
的延长线于点 ,交
,交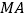 于点
于点 ,连接
,连接 ,交
,交 于点
于点 ,连接
,连接 ,若
,若 ,求点
,求点 的横坐标.
的横坐标.
相关试题

