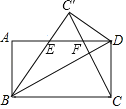
【题目】如图,将矩形ABCD沿对角线BD折叠,点C的对应点为点C′,连接CC′交AD于点F,BC′与AD交于点E.
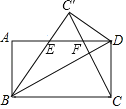
(1)求证:△BAE≌△DC′E;
(2)写出AE与EF之间的数量关系,并说明理由;
(3)若CD=2DF=4,求矩形ABCD的面积.
参考答案:
【答案】(1)见解析;(2)AE=EF,见解析;(3)S矩形ABCD=32.
【解析】
(1)根据AAS证明△BAE≌△DC′E即可.
(2)证明AE=EC′,EC′=EF即可.
(3)证明△CDF∽△BCD,再利用相似三角形的性质求出BC即可解决问题.
解:(1)证明:∵四边形ABCD是矩形,
∴AB=CD,∠A=∠BCD=90°
由翻折的性质可知:CD=C′D,∠BCD=∠BC′D=90°,
∴∠A=∠DC′E=90°,AB=C′D,
∵∠AEB=∠DEC′,
∴△BAE≌△DC′E(AAS).
(2)解:结论:AE=EF.
理由:∵△BAE≌△DC′E,
∴AE=EC′,
∵BC=BC′,
∴∠BCC′=∠BC′C,
∵EF∥BC,
∴∠EFC′=∠BCC′,
∴∠EC′F=∠EFC′,
∴EF=EC′,
∴AE=EF.
(3)解:由翻折可知:BD⊥CC′,
∴∠FCD+∠BDC=90°,∠BDC+∠CBD=90°,
∴∠FCD=∠CBD,
∵∠CDF=∠BCD=90°,
∴△CDF∽△BCD,
∴![]() ,
,
∴![]() ,
,
∴BC=8,
∴S矩形ABCD=BCCD=32.
-
科目: 来源: 题型:
查看答案和解析>>【题目】又到一年丰收季,重庆外国语学校“国内中考、高考、国内保送、出国留学”捷报频传.作为准初三的初二年级学生希望抓紧暑期更好的提升自我.张同学采用随机抽样的方式对初二年级学生此次暑期生活的主要计划进行了问卷调查,并将调查结果按照“A社会实践类、B学习提高类、C游艺娱乐类、D其他”进行了分类统计,并绘制了如图1和如图2两幅不完整的统计图.(接受调查的每名同学只能在四类中选择其中一种类型,不可多选或不选.)请根据图中提供的信息完成以下问题.
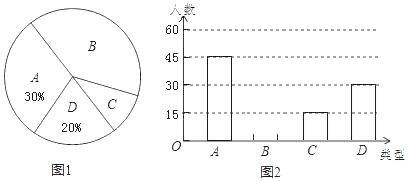
(1)扇形统计图中表示B类的扇形的圆心角是 度,并补全条形统计图;
(2)张同学已从被调查的同学中确定了甲、乙、丙、丁四名同学进行开学后的经验交流,并计划在这四人中选出两人的宝贵经验刊登在本班班刊上.请利用画树状图或列表的方法求出甲同学的经验刊登在班刊上的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于
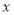 的不等式组
的不等式组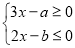 的整数解仅有
的整数解仅有 ,
,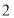 ,那么适合这个不等式组的整数
,那么适合这个不等式组的整数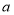 ,
,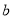 组成的有序数对
组成的有序数对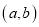 共有_______个;如果关于
共有_______个;如果关于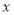 的不等式组
的不等式组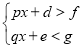 (其中
(其中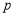 ,
,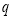 为正整数)的整数解仅有
为正整数)的整数解仅有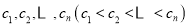 ,那么适合这个不等式组的整数
,那么适合这个不等式组的整数 ,
,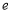 组成的有序数对
组成的有序数对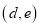 共有______个.(请用含
共有______个.(请用含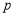 、
、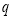 的代数式表示)
的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是( )
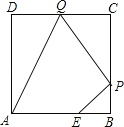
A. 3 B. 5 C. 4 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系xOy中,矩形ABCD的DC边在x轴上,D点坐标为(﹣6,0)边AB、AD的长分别为3、8,E是BC的中点,反比例函数y=
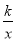 的图象经过点E,与AD边交于点F.
的图象经过点E,与AD边交于点F.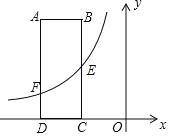
(1)求k的值及经过A、E两点的一次函数的表达式;
(2)若x轴上有一点P,使PE+PF的值最小,试求出点P的坐标;
(3)在(2)的条件下,连接EF、PE、PF,在直线AE上找一点Q,使得S△QEF=S△PEF直接写出符合条件的Q点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,P为Rt△ABC外一点,且∠BPC=60°,过点A作AD⊥PC交PC于点D,连接BD,若∠PDB=45°,BD=
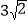 ,则PC= _____.
,则PC= _____.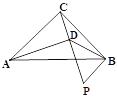
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:方程组
 的解x为非正数,y为负数.
的解x为非正数,y为负数.(1)求a的取值范围;
(2)化简|a-3|+|a+2|;
(3)在a的取值范围中,当a为何整数时,不等式2ax+x>2a+1的解为x<1.
相关试题

