【题目】如图,在直角坐标系xOy中,矩形ABCD的DC边在x轴上,D点坐标为(﹣6,0)边AB、AD的长分别为3、8,E是BC的中点,反比例函数y=![]() 的图象经过点E,与AD边交于点F.
的图象经过点E,与AD边交于点F.
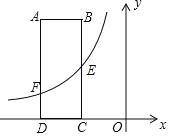
(1)求k的值及经过A、E两点的一次函数的表达式;
(2)若x轴上有一点P,使PE+PF的值最小,试求出点P的坐标;
(3)在(2)的条件下,连接EF、PE、PF,在直线AE上找一点Q,使得S△QEF=S△PEF直接写出符合条件的Q点坐标.
参考答案:
【答案】(1)k=-12,y=﹣![]() x;(2)P(﹣5,0);(3)Q(﹣
x;(2)P(﹣5,0);(3)Q(﹣![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).
【解析】
(1)先确定点B,C坐标,进而得出点E坐标,最后用待定系数法即可求出直线AE解析式;
(2)先找出点F关于x轴的对称点F′的坐标,进而求出直线EF′的解析式,进一步即可得出结论;
(3)先求出△PEF的面积,再求出直线EF的解析式,设出点Q的坐标,利用坐标系中求三角形面积的方法建立方程求解,进而得出结论.
解:(1)在矩形ABCD中,AB=3,AD=8,
∴CD=AB=3,BC=AD=8,
∵D(﹣6,0),
∴A(﹣6,8),C(﹣3,0),B(﹣3,8),
∵E是BC的中点,
∴E(﹣3,4),
∵点E在反比例函数y=![]() 的图象上,
的图象上,
∴k=﹣3×4=﹣12,
设经过A、E两点的一次函数的表达式为y=k′x+b,
∴![]() ,解得
,解得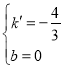 ,
,
∴经过A、E两点的一次函数的表达式为y=﹣![]() x;
x;
(2)如图1,由(1)知,k=﹣12,
∴反比例函数的解析式为y=﹣![]() ,
,
∵点F的横坐标为﹣6,∴点F的纵坐标为2,∴F(﹣6,2),
作点F关于x轴的对称点F′,则F′(﹣6,﹣2),
连接EF′交x轴于点P,此时,PE+PF的值最小,
∵E(﹣3,4),
∴直线EF′的解析式为y=2x+10,
令y=0,则2x+10=0,解得x=﹣5,
∴P(﹣5,0);

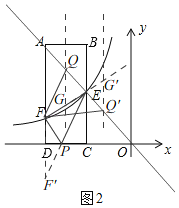
(3)如图2,由(2)知,F′(﹣6,﹣2),
∵E(﹣3,4),F(﹣6,2),
∴S△PEF=S△EFF′﹣S△PFF′=![]() ×(2+2)×(﹣3+6)﹣
×(2+2)×(﹣3+6)﹣![]() (2+2)×(﹣5+6)=4,
(2+2)×(﹣5+6)=4,
∵E(﹣3,4),F(﹣6,2),
∴直线EF的解析式为y=![]() x+6,
x+6,
由(1)知,经过A、E两点的一次函数的表达式为y=﹣![]() x,
x,
设点Q(m,﹣![]() m),
m),
过点Q作y轴的平行线交EF于G,
∴G(m,![]() m+6),
m+6),
∴QG=|﹣![]() m﹣
m﹣![]() m﹣6|=|2m+6|,
m﹣6|=|2m+6|,
∵S△QEF=S△PEF,
∴S△QEF=![]() |2m+6|×(﹣3+6)=4,
|2m+6|×(﹣3+6)=4,
∴m=﹣![]() 或m=﹣
或m=﹣![]() ,
,
∴Q(﹣![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于
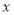 的不等式组
的不等式组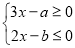 的整数解仅有
的整数解仅有 ,
,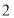 ,那么适合这个不等式组的整数
,那么适合这个不等式组的整数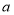 ,
,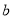 组成的有序数对
组成的有序数对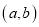 共有_______个;如果关于
共有_______个;如果关于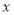 的不等式组
的不等式组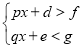 (其中
(其中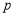 ,
,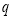 为正整数)的整数解仅有
为正整数)的整数解仅有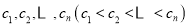 ,那么适合这个不等式组的整数
,那么适合这个不等式组的整数 ,
,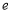 组成的有序数对
组成的有序数对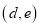 共有______个.(请用含
共有______个.(请用含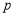 、
、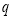 的代数式表示)
的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是( )
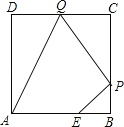
A. 3 B. 5 C. 4 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿对角线BD折叠,点C的对应点为点C′,连接CC′交AD于点F,BC′与AD交于点E.
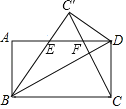
(1)求证:△BAE≌△DC′E;
(2)写出AE与EF之间的数量关系,并说明理由;
(3)若CD=2DF=4,求矩形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,P为Rt△ABC外一点,且∠BPC=60°,过点A作AD⊥PC交PC于点D,连接BD,若∠PDB=45°,BD=
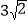 ,则PC= _____.
,则PC= _____.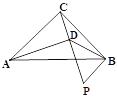
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:方程组
 的解x为非正数,y为负数.
的解x为非正数,y为负数.(1)求a的取值范围;
(2)化简|a-3|+|a+2|;
(3)在a的取值范围中,当a为何整数时,不等式2ax+x>2a+1的解为x<1.
-
科目: 来源: 题型:
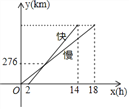
查看答案和解析>>【题目】如图是一辆慢车与一辆快车沿相同路线从
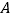 地到
地到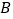 地所行的路程与时间之间的函数图象,已知慢车比快车早出发
地所行的路程与时间之间的函数图象,已知慢车比快车早出发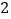 小时,则
小时,则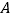 、
、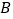 两地的距离为________
两地的距离为________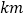 .
.
相关试题

