【题目】从共享单车,共享汽车等共享出行到共享雨伞等共享物品,各式各样的共享
经济模式在各个领域迅速的普及。
(1) 为获得泰州市市民参与共享经济的活动信息,下列调查方式中比较合理的是 ;
A.对某学校的全体同学进行问卷调查 B.对某小区的住户进行问卷调查
C.在全市里的不同区县,选取部分市民进行问卷调查
(2) 调查小组随机调查了泰兴市市民骑共享单车情况,某社区年龄在12~36岁的人有1000人,从中随机抽取了100人,统计了他们骑共享单车的人数,并绘制了如下不完整的统计图表.

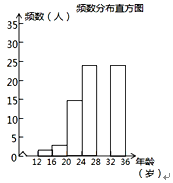
根据以上信息解答下列问题:
① 求出统计表中的a、b,并补全频数分布直方图
② 试估计这个社区年龄在20岁到32岁(含20岁,不含32岁)骑共享单车的人有多少人?
参考答案:
【答案】(1)C ;(2)a=0.15,b=30,;(3)700人
【解析】分析: (1)根据抽样调查与普查的意义可得;
(2)①根据“频率=频数÷总数”可分别求得a、b的值;由①中所求数据可补全图形;
②总人数乘以样本中第3、4、5组的频率之和可得答案.
详解: (1)∵泰州市市民参与共享经济的活动信息工作量比较大,
∴宜采用抽样调查的方法,即在全市里的不同区县,选取部分市民进行问卷调查.
故选C.
(2)①a=15÷100=0.15,b=100×0.3=30;如图,
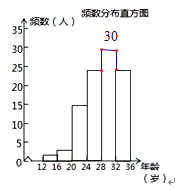
②1000×(0.15+0.25+0.3)=700(人),
答:估计这个社区年龄在20岁到32岁(含20岁,不含32岁)骑共享单车的人有700人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】金桥学校“科技体艺节”期间,八年级数学活动小组的任务是测量学校旗杆AB的高,他们在旗杆正前方台阶上的点C处,测得旗杆顶端A的仰角为45°,朝着旗杆的方向走到台阶下的点F处,测得旗杆顶端A的仰角为60°,已知升旗台的高度BE为1米,点C距地面的高度CD为3米,台阶CF的坡角为30°,且点E、F、D在同一条直线上,求旗杆AB的高度(计算结果精确到0.1米,参考数据:
 ≈1.41,
≈1.41, 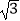 ≈1.73)
≈1.73)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O.
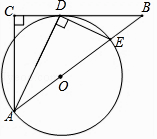
(1)求证:BC是⊙O的切线;
(2)若AC=3,BC=4,求BE的长. -
科目: 来源: 题型:
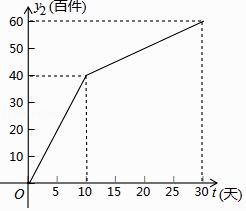
查看答案和解析>>【题目】我市雷雷服饰有限公司生产了一款夏季服装,通过实体商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量y1(百件)与时间t(t为整数,单位:天)的部分对应值如下表所示,网上商店的日销售量y2(百件)与时间t(t为整数,单位:天)的部分对应值如图所示.
时间t(天)
0
5
10
15
20
25
30
日销售量
y1(百件)0
25
40
45
40
25
0
(1)请你在一次函数、二次函数和反比例函数中,选择合适的函数能反映y1与t的变化规律,并求出y1与t的函数关系式及自变量t的取值范围;
(2)求y2与t的函数关系式,并写出自变量t的取值范围;
(3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为y(百件),求y与t的函数关系式;当t为何值时,日销售总量y达到最大,并求出此时的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(9分)如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若A的对应点A2的坐标为(0,4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,在平面直角坐标系xOy中,∠C=90°,OB=25,OC=20,若点M是边OC上的一个动点(与点O、C不重合),过点M作MN∥OB交BC于点N.

(1)求点C的坐标;
(2)当△MCN的周长与四边形OMNB的周长相等时,求CM的长;
(3)在OB上是否存在点Q,使得△MNQ为等腰直角三角形?若存在,请求出此时MN的长;若不存在,请说明理由. -
科目: 来源: 题型:
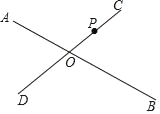
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,P是CD上一点,
(1)过点P作AB的垂线段PE;
(2)过点P作CD的垂线,与AB相交于点F;
(3)将线段PE、PF、FO从小到大排列为_____,这样排列的依据是_____.
相关试题

