【题目】如图,已知一条直线过点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() 两点,其中点
两点,其中点![]() 的横坐标是
的横坐标是![]() .
.
⑴求这条直线的函数关系式及点![]() 的坐标 ;
的坐标 ;
⑵在![]() 轴上是否存在点
轴上是否存在点![]() ,使得△
,使得△![]() 是直角三角形?若存在,求出点
是直角三角形?若存在,求出点![]() 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
⑶过线段![]() 上一点
上一点![]() ,作
,作![]() ∥
∥![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,点
,点![]() 在第一象限;点
在第一象限;点![]() ,当点
,当点![]() 的横坐标为何值时,
的横坐标为何值时, ![]() 的长度最大?最大值是多少?
的长度最大?最大值是多少?

参考答案:
【答案】(1)点![]() 的坐标为
的坐标为![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 的横坐标为6时,
的横坐标为6时, ![]() 的长度最大值为18.
的长度最大值为18.
【解析】⑴关键是求直线的解析式,由于直线上有一点为![]() ,所以再找一个点即可求出直线的解析式;
,所以再找一个点即可求出直线的解析式; ![]() 的横坐标是
的横坐标是![]() 代入抛物线的解析式即可求出它的纵坐标,利用待定系数法可求直线的函数关系式;由于点
代入抛物线的解析式即可求出它的纵坐标,利用待定系数法可求直线的函数关系式;由于点![]() 是两个函数图象的交点,所以把两个函数联立起来,利用方程思想可以解决问题.
是两个函数图象的交点,所以把两个函数联立起来,利用方程思想可以解决问题.
⑵先假设存在,在假设存在的情况下还要分类讨论,因为没有指明直角顶点,所以要分成三种情况来讨论,利用勾股定理建立方程可以解决问题.
⑶利用![]() 的横坐标分别表示出线段
的横坐标分别表示出线段![]() 的长度,再利用
的长度,再利用![]() 建立函数关系,再根据函数关系来求最值.
建立函数关系,再根据函数关系来求最值.
解:⑴∵直线与抛物线交点![]() 的横坐标是
的横坐标是![]() ,
,
∴![]() ,
,
∴点![]() 的坐标是
的坐标是![]()
设此直线的解析式为![]() ,
,
将![]() 代入得
代入得![]() ,
,
解得: 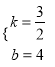 ,
,
∴此直线的解析式为![]() .
.
∵直线和抛物线交于![]() 两点,
两点,
∴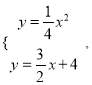
解得: ![]() 或
或![]()
∴点![]() 的坐标为
的坐标为![]() .
.
⑵.如备用图,点![]() 在
在![]() 轴上,连接
轴上,连接![]() .
.
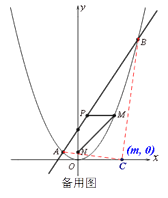
∵![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,
若设存在的点![]() 的坐标为
的坐标为![]() ,则:
,则:
![]() ,
,
![]() ,
,
①.当![]() 时,
时, ![]() ,即
,即![]() ,
,
解得: ![]() .
.
②.当![]() 时,
时, ![]() ,即
,即![]()
解得: ![]() 或
或![]() .
.
③.当![]() 时,
时, ![]() ,即
,即![]()
解得: ![]() .
.
∴求出点![]() 的坐标为
的坐标为![]() .
.
⑶.设点![]() ,设
,设![]() 与
与![]() 轴的交点为
轴的交点为![]() ;
;
在![]() △
△![]() 中,由勾股定理的:
中,由勾股定理的: 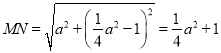 ,
,
又∵点![]() 与点
与点![]() 的纵坐标相同,∴
的纵坐标相同,∴![]() ,
,
∴![]() ,即点
,即点![]() 的横坐标为
的横坐标为![]() ,
,
∴![]() ,
,
∴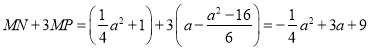 ,
,
∴当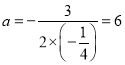 时,又∵
时,又∵![]() ,取值最大值取到18.
,取值最大值取到18.
∴当![]() 的横坐标为6时,
的横坐标为6时, ![]() 的长度最大值为18.
的长度最大值为18.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D是△ABC的边AB上一点,CE∥AB,DE交AC于点F,若FA=FC.
(1)求证:四边形ADCE是平行四边形;
(2)若AE⊥EC,EF=EC=5,求四边形ADCE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是弧
 的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.
的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.⑴求证:AC=CD.
⑵若OB=2,求BH的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列方程及解的特征:
(1)x+
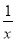 =2的解为x1=x2=1;
=2的解为x1=x2=1;(2)x+
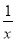 =
=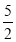 的解为x1=2,x2=
的解为x1=2,x2=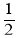 ;
;(3)x+
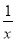 =
=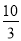 的解为x1=3,x2=
的解为x1=3,x2=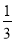 ;
; …
解答下列问题:
(1)请猜想:方程x+
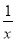 =
=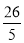 的解为______;
的解为______;(2)请猜想:关于x的方程x+
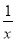 =______ 的解为x1=a,x2=
=______ 的解为x1=a,x2=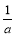 (a≠0);
(a≠0);(3)下面以解方程x+
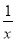 =
=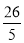 为例,验证(1)中猜想结论的正确性.
为例,验证(1)中猜想结论的正确性.(4)解方式方程

-
科目: 来源: 题型:
查看答案和解析>>【题目】据报道,截止到2013年12月31日我国微信用户规模已达到6亿.以下是根据相关数据制作的统计图表的一部分:2012年及2013年电话、短信、微信的截止到2013年12月31日微信用户对日人均使用时长统计表 单位:分钟

“微信公众平台”参与关注度统计图

请根据以上信息,回答以下问题:
(1)从2012年到2013年微信的日人均使用时长增加了 分钟;
(2)截止到2013年12月31日,在我国6亿微信用户中偶尔使用微信用户约为 亿(结果精确到0.1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中O是原点,平行四边形ABCO的顶点A、C的坐标分别(8,0)、(3,4),点D,E把线段OB三等分,延长CD、CE分别交OA、AB于点F,G,连接FG.则下列结论:①F是OA的中点;②△OFD与△BEG相似;③四边形DEGF的面积是
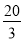 ;④
;④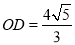 .正确的个数是( )
.正确的个数是( )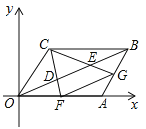
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,长方形ABCD中分别沿AF、CE将AC两侧折叠,使点B、D分别落在AC上的G、H处,则线段AE______CF.(填“>”“<”或“=”)
(2)如图2,在平行四边形ABCD中,△ABF≌△CDE,AB=10cm,BF=6cm,AF=8cm,动点P、Q分别从A、C两点同时出发,点P自A→F→B→A停止,点Q自C→D→E→C停止.
①若点P的速度为每秒5cm,点Q的速度为每秒4cm,设运动时间为t秒.当点P在FB上运动,而点Q在DE上运动时,若四边形APCQ是平行四边形,求此时t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),利用备用图探究,当a与b满足什么数量关系时,四边形APCQ是平行四边形.
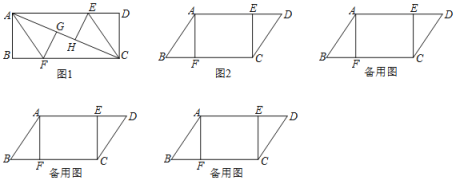
相关试题

