搜索
【题目】如图，在平面直角坐标系xOy中，点B（－1，4），点A（－7，0），点P是直线
上一点，且∠ABP＝45°，则点P的坐标为____.
参考答案：
【答案】(-
,-
)
【解析】
过点A作AH⊥BA,交BP于H,过点A作x轴的垂线,作BM⊥AM,HN⊥AN,求出直线BH的解析式，然后与
联立方程组，求解即可.
过点A作AH⊥BA,交BP于H,过点A作x轴的垂线,作BM⊥AM,HN⊥AN,
∵∠ABP＝45°
∴AB=AH
∵根据直角三角形性质得：∠AMB=∠ANH, ∠MBA=∠NAH,
∴△BMA≌△ANH,
∴AN=BM=-1-（-7）=6，NH=AM=4 ,
∴H的横坐标是：-7+4=-3
∴H(-3,-6),
设直线BH为y=kx+b
把H(-3,-6), B(-1,4)代入得
解得
∴直线BH为：y=5x+9
∴y=5x+9与联立方程组为
，
解得：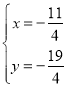
，即P(-
,-
).
-
科目： 来源： 题型：
查看答案和解析>>【题目】一袋中装有形状大小都相同的四个小球，每个小球上各标有一个数字，分别是1，4，7，8．现规定从袋中任取一个小球，对应的数字作为一个两位数的个位数；然后将小球放回袋中并搅拌均匀，再任取一个小球，对应的数字作为这个两位数的十位数．
（1）写出按上述规定得到所有可能的两位数；
（2）从这些两位数中任取一个，求其算术平方根大于4且小于7的概率．
-
科目： 来源： 题型：
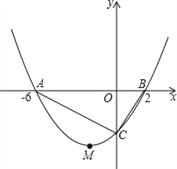
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c的顶点为M（﹣2,﹣4），与x轴交于A、B两点,且A（﹣6,0），与y轴交于点C．
（1）求抛物线的函数解析式；
（2）求△ABC的面积；
（3）能否在抛物线第三象限的图象上找到一点P,使△APC的面积最大？若能,请求出点P的坐标；若不能，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】“端午节”期间，某商场购进A、B两种品牌的粽子共320袋，其中A品牌比B品牌多80袋．此两种粽子每袋的进价和售价如下表所示，已知销售八袋A品牌的粽子获利136元．(注；利润=售价-进价)
品牌
A
B
进价(元/袋)
m
38
售价(元/袋)
66
50
(1)试求出m的值．
(2)该商场购进A、B两种品牌的粽子各多少袋？
(3)该商场调整销售策略，A品牌的粽子每袋按原售价销售，B品牌的粽子每袋打折出售.如果购进的A、B两种品牌的粽子全部售出的利润不少于4360元，问B种品牌的粽子每袋最低打几折出售？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图（1），已知正方形ABCD在直线MN的上方，BC在直线MN上，E是BC上一点，以AE为边在直线MN的上方作正方形AEFG．
（1）连接GD，求证：△ADG≌△ABE；
（2）连接FC，观察并猜测∠FCN的度数，并说明理由；
（3）如图（2），将图（1）中正方形ABCD改为矩形ABCD，AB=a，BC=b（a、b为常数），E是线段BC上一动点（不含端点B、C），以AE为边在直线MN的上方作矩形AEFG，使顶点G恰好落在射线CD上．判断当点E由B向C运动时，∠FCN的大小是否总保持不变？若∠FCN的大小不变，请用含a、b的代数式表示tan∠FCN的值；若∠FCN的大小发生改变，请举例说明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商家用1200元购进了一批T恤，上市后很快售完，商家又用2800元购进了第二批这种T恤，所购数量是第一批购进量的2倍，但单价贵了5元．
（1）该商家购进的第一批T恤是多少件？
（2）若两批T恤按相同的标价销售，最后剩下20件按八折优惠卖出，如果希望两批T恤全部售完的利润率不低于16%（不考虑其它因素），那么每件T恤的标价至少是多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将
绕着点B顺时针旋转至
，使得C点落在AB的延长线上的D点处，的边BC恰好是
的角平分线.(1)试求旋转角
的度数；(2)设BE与AC的交点为点P，求证：
．
相关试题
