【题目】如图,直线EF与MN相交于点O,∠MOE=30°,将一直角三角尺的直角顶点与点O重合,直角边OA与MN重合,OB在∠NOE内部.操作:将三角尺绕点O以每秒5°的速度沿顺时针方向旋转一周,设运动时间为t(s).
(1)当t为何值时,直角边OB恰好平分∠NOE?此时OA是否平分∠MOE?请说明理由;
(2)若在三角尺转动的同时,直线EF也绕点O以每秒8°的速度顺时针方向旋转一周,当一方先完成旋转一周时,另一方同时停止转动.
①当t为何值时,OE平分∠AOB?
②OE能否平分∠NOB?若能请直接写出t的值;若不能,请说明理由.

参考答案:
【答案】(1)t=3,此时OA平分∠MOE;(2)①t=5;②t=![]() .
.
【解析】
(1)根据:角度=速度×时间进行计算,由等量关系:直角边OB恰好平分∠NOE,列出方程求解即可.
(2)①用t表示∠AOE的度数令其等于45°即可求;
②用t表示∠NOE、∠BOE的度数然后列方程解决.
(1)∵当直角边OB恰好平分∠NOE时,∠NOB= ![]() ∠NOE=
∠NOE= ![]() (180°﹣30°)=75°,
(180°﹣30°)=75°,
∴90﹣5t=75,
解得:t=3,
此时∠MOA=5°×3=15°= ![]() ∠MOE,
∠MOE,
∴此时OA平分∠MOE.
(2)①若OE平分∠AOB,
由题意得 30+8t﹣5t=90÷2,
解得 t=5;
②若OE平分∠NOB上面,
由题意得180﹣(30°+8t)= ![]() (90﹣5t),
(90﹣5t),
解得t=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为完善人口发展战略,我国现已全面提倡实施一对夫妇可生育两个孩子的政策.某中学为了解在校生对父母再生“二胎”的同意情况,在校园内随机调查了部分学生对“二胎”的同意情况(把调查的结果分为四个等级:A非常同意;B:同意;C:无所谓;D:坚决反对),并将调查结果绘成了如下两幅不完整的统计图. 请根据统计图中的信息解答下列问题:
(1)本次被抽样调查的学生有多少人?
(2)将两幅统计图补充完整:
(3)若全校共有3600名学生,估计“非常同意“父母再生“二胎”的大约有多少人?
(4)若从3名“同意”父母生“二胎”和2名“坚决反对”父母生“二胎”的学生中随机抽取两名学生,用树状图或列表法求抽取的两个恰好都“坚决反对”父母生“二胎”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
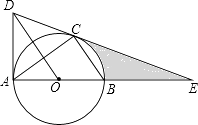
(1)判断DE与⊙O的位置关系,并证明你的结论;
(2)若AE=6,CE=2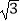 . ①求⊙O的半径
. ①求⊙O的半径
②求线段CE,BE与劣弧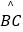 所围成的图形的面积(结果保留根号和π)
所围成的图形的面积(结果保留根号和π) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是( )
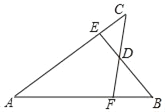
A. ① B. ② C. ①和② D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年9月,莉莉进入八中初一,在准备开学用品时,她决定购买若干个某款笔记本,甲、乙两家文具店都有足够数量的该款笔记本,这两家文具店该款笔记本标价都是20元/个.甲文具店的销售方案是:购买该笔记本的数量不超过5个时,原价销售;购买该笔记本超过5个时,从第6个开始按标价的八折出售:乙文具店的销售方案是:不管购买多少个该款笔记本,一律按标价的九折出售.
(1)若设莉莉要购买x(x>5)个该款笔记本,请用含x的代数式分别表示莉莉到甲文具店和乙文具店购买全部该款笔记本所需的费用;
(2)在(1)的条件下,莉莉购买多少个笔记本时,到乙文具店购买全部笔记本所需的费用与到甲文具店购买全部笔记本所需的费用相同?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明在大楼45米高(即PH=45米)的窗户P处进行观测,测得山坡上A处的俯角为15°,山脚B处得俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:
 .点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上且PH⊥HC,求A、B两点间的距离(结果精确到0.1米,参考数据:
.点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上且PH⊥HC,求A、B两点间的距离(结果精确到0.1米,参考数据:  ≈1.732.
≈1.732.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场欲购进果汁饮料和碳酸饮料共50箱,两种饮料每箱进价和售价如下表所示:
饮料
果汁饮料
碳酸饮料
进价(元/箱)
55
36
售价(元/箱)
63
42
设购进果汁饮料x箱(x为正整数),且所购进的两种饮料能全部卖出,获得的总利润为w元(注:总利润=总售价﹣总进价).
(1)求总利润w关于x的函数关系式;
(2)如果购进两种饮料的总费用不超过2000元,那么该商场如何进货才能获利最多?并求出最大利润.
相关试题

