【题目】某商场欲购进果汁饮料和碳酸饮料共50箱,两种饮料每箱进价和售价如下表所示:
饮料 | 果汁饮料 | 碳酸饮料 |
进价(元/箱) | 55 | 36 |
售价(元/箱) | 63 | 42 |
设购进果汁饮料x箱(x为正整数),且所购进的两种饮料能全部卖出,获得的总利润为w元(注:总利润=总售价﹣总进价).
(1)求总利润w关于x的函数关系式;
(2)如果购进两种饮料的总费用不超过2000元,那么该商场如何进货才能获利最多?并求出最大利润.
参考答案:
【答案】
(1)解:由题意可得,
w=(63﹣55)x+(42﹣36)(50﹣x)=2x+300,
即总利润w关于x的函数关系式是w=2x+300
(2)解:由题意可得,
55x+36(50﹣x)≤2000,
解得,x≤ ![]() ,
,
∴当x=10时,w取得最大值,此时w=2×10+300=320,
即该商场果汁饮料10箱,碳酸饮料40箱,获得利润最多,最大利润为320元
【解析】(1)根据题意可以得到w关于x的函数关系式,本题得以解决;(2)根据题意可以得到相应的不等式,从而可以求得w的最大值,本题得以解决.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线EF与MN相交于点O,∠MOE=30°,将一直角三角尺的直角顶点与点O重合,直角边OA与MN重合,OB在∠NOE内部.操作:将三角尺绕点O以每秒5°的速度沿顺时针方向旋转一周,设运动时间为t(s).
(1)当t为何值时,直角边OB恰好平分∠NOE?此时OA是否平分∠MOE?请说明理由;
(2)若在三角尺转动的同时,直线EF也绕点O以每秒8°的速度顺时针方向旋转一周,当一方先完成旋转一周时,另一方同时停止转动.
①当t为何值时,OE平分∠AOB?
②OE能否平分∠NOB?若能请直接写出t的值;若不能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】今年9月,莉莉进入八中初一,在准备开学用品时,她决定购买若干个某款笔记本,甲、乙两家文具店都有足够数量的该款笔记本,这两家文具店该款笔记本标价都是20元/个.甲文具店的销售方案是:购买该笔记本的数量不超过5个时,原价销售;购买该笔记本超过5个时,从第6个开始按标价的八折出售:乙文具店的销售方案是:不管购买多少个该款笔记本,一律按标价的九折出售.
(1)若设莉莉要购买x(x>5)个该款笔记本,请用含x的代数式分别表示莉莉到甲文具店和乙文具店购买全部该款笔记本所需的费用;
(2)在(1)的条件下,莉莉购买多少个笔记本时,到乙文具店购买全部笔记本所需的费用与到甲文具店购买全部笔记本所需的费用相同?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明在大楼45米高(即PH=45米)的窗户P处进行观测,测得山坡上A处的俯角为15°,山脚B处得俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:
 .点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上且PH⊥HC,求A、B两点间的距离(结果精确到0.1米,参考数据:
.点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上且PH⊥HC,求A、B两点间的距离(结果精确到0.1米,参考数据:  ≈1.732.
≈1.732.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为-20,点B表示的数为16.动点P从点A出发,以每秒6个单位长度的速度沿数轴向右匀速运动,动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动.若点P、Q同时出发,设运动时间为t(t>0)秒.
(1)填空:①点A、B之间的距离为 ;
②点P表示的数为 ,点Q表示的数为 (用含t的代数式表示);
(2)当点P、Q到原点O的距离相等时,求t的值并求出此时点Q表示的数;
(3)若点P从点A出发到达点B后立刻返回到点A并保持速度不变,点Q到达点A时停止运动,问点P运动多少秒时与点Q相距6个单位长度?


-
科目: 来源: 题型:
查看答案和解析>>【题目】设一列数
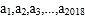 中任意三个相邻的数之和都是22,已知
中任意三个相邻的数之和都是22,已知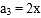 ,
,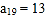 ,
,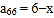 ,那么
,那么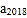 =________.
=________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB于E点,DF⊥AC于F点,有下列结论:①BD=DC;②DE=DF;③AD上任意一点到AB,AC的距离相等;④AD上任意一点到B点与C点的距离不等.其中正确的是( )

A. ①② B. ③④ C. ①②③ D. ①②③④
相关试题

