【题目】如图,△ABC中任意一点P(x0,y0)经过平移后对应点为P1(x0+4,y0-1).
(1)画出△ABC作同样的平移后得到的△A1B1C1,并写出A1、B1、C1的坐标.
(2)以点P1为位似中心,画出△A1B1C1的一个位似△A2B2C2,使它与△A1B1C1的相似比为2:1. 并写出A2、B2、C2的坐标.

参考答案:
【答案】(1)画图见解析, A1(0,1)、B1(1,-2)、C1(3,2)
(2)画图见解析A2(-1,2)、B2(1,-4)、C2(5,4)
【解析】试题分析:(1)根据平移规律,横坐标加上4,纵坐标减去1,先找出平移后的点A1、B1、C1的坐标位置,然后顺次连接即可得到△A1B1C1,然后根据平面直角坐标系写出点的坐标即可;
(2)延长P1A1到A2,使P1A2=2P1A1,延长P1B1到B2,使P1B2=2P1B1,延长P1C1到C2,使P1C2=2P1C1,顺次连接A2、B2、C2即可得到△A2B2C2,然后根据平面直角坐标系写出点的坐标即可.
试题解析:(1)如图所示,△A1B1C1即为所求作的三角形,
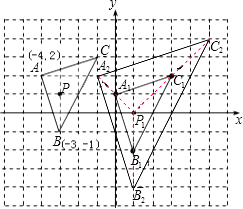
点A1(0,1),B1(1,-2),C1(3,2);
(2)△A2B2C2即为所求作的三角形,
点A2(-1,2),B2(1,-4),C2(5,4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.(﹣2ab)?(﹣3ab)3=﹣54a4b4
B.5x2?(3x3)2=15x12
C.(﹣0.1 b)?(﹣10b2)3=﹣b7
D.(2×10n)( ×10n)=102n
×10n)=102n -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是 . (把所有正确结论的序号都填在横线上) ①∠DCF=
 ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个直角三角形中,有一个锐角等于30°,则另一个锐角的大小为______度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)一个不透明的盒子中,装有2个白球和1个红球,这些球除颜色外其余都相同.
(1)小明认为,搅均后从中任意摸出一个球,不是白球就是红球,因此模出白球和模出红球这两个事件是等可能的. 你同意他的说法吗?为什么?
(2)搅均后从中一把模出两个球,请通过树状图或列表,求两个球都是白球的概率;
(3)搅均后从中任意模出一个球,要使模出红球的概率为
 ,应如何添加红球?
,应如何添加红球? -
科目: 来源: 题型:
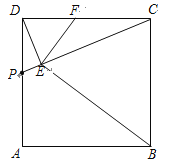
查看答案和解析>>【题目】如图,正方形ABCD中,点P是AD上的一动点(与点D、点A不重合),DE⊥CP,垂足为E,EF⊥BE与DC交于点F.
(1)求证:△DEF∽△CEB;
(2)当点P运动到DA的中点时,求证:点F为DC的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)某中学九年级学生在学习“直角三角形的边角关系”时,组织开展测量物体高度的实践活动.在活动中,某小组为了测量校园内①号楼AB的高度(如图),站在②号楼的C处,测得①号楼顶部A的仰角α=30°,底部B的俯角β=45°.已知两幢楼的水平距离BD为18米,求①号楼AB的高度.(结果保留根号)

相关试题

