Question

【题目】如图，在ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论中一定成立的是 ． （把所有正确结论的序号都填在横线上） ①∠DCF= ∠BCD；②EF=CF；③S△BEC=2S△CEF；④∠DFE=3∠AEF．

Answer 1

【答案】①②④
【解析】解：①∵F是AD的中点， ∴AF=FD，
∵在ABCD中，AD=2AB，
∴AF=FD=CD，
∴∠DFC=∠DCF，
∵AD∥BC，
∴∠DFC=∠FCB，
∴∠DCF=∠BCF，
∴∠DCF= ∠BCD，故此选项正确；
延长EF，交CD延长线于M，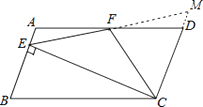

∵四边形ABCD是平行四边形，
∴AB∥CD，
∴∠A=∠MDF，
∵F为AD中点，
∴AF=FD，
在△AEF和△DFM中，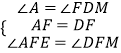
，
∴△AEF≌△DMF（ASA），
∴FE=MF，∠AEF=∠M，
∵CE⊥AB，
∴∠AEC=90°，
∴∠AEC=∠ECD=90°，
∵FM=EF，
∴FC=FM，故②正确；
③∵EF=FM，
∴S△EFC=S△CFM ，
∵MC＞BE，
∴S△BEC＜2S△EFC
故S△BEC=2S△CEF错误；
④设∠FEC=x，则∠FCE=x，
∴∠DCF=∠DFC=90°﹣x，
∴∠EFC=180°﹣2x，
∴∠EFD=90°﹣x+180°﹣2x=270°﹣3x，
∵∠AEF=90°﹣x，
∴∠DFE=3∠AEF，故此选项正确．
所以答案是：①②④．
【考点精析】根据题目的已知条件，利用直角三角形斜边上的中线和平行四边形的性质的相关知识可以得到问题的答案，需要掌握直角三角形斜边上的中线等于斜边的一半；平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分．