【题目】如图,平行四边形 ABCD 中,AD∥BC,AB=BC=CD=AD=4,∠A=∠C=60°,连接 BD,将△BCD 绕点 B 旋转,当 BD(即 BD′)与 AD 交于一点 E,BC(即 BC′)同时与 CD 交于一点 F 时,下列结论正确的是( )
①AE=DF;②∠BEF=60°;③∠DEB=∠DFB;④△DEF 的周长的最小值是4+2![]()
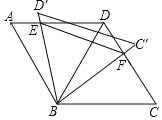
A. ①② B. ②③ C. ①②④ D. ①②③④
参考答案:
【答案】C
【解析】
根据题意可证△ABE≌△BDF,可判断①②③,由△DEF的周长=DE+DF+EF=AD+EF=4+EF,则当EF最小时△DEF的周长最小,根据垂线段最短,可得BE⊥AD时,BE最小,即EF最小,即可求此时△BDE周长最小值.
∵AB=BC=CD=AD=4,∠A=∠C=60°,
∴△ABD,△BCD为等边三角形,∴∠A=∠BDC=60°.
∵将△BCD绕点B旋转到△BC'D'位置,
∴∠ABD'=∠DBC',且AB=BD,∠A=∠DBC',
∴△ABE≌△BFD,
∴AE=DF,BE=BF,∠AEB=∠BFD,
∴∠BED+∠BFD=180°.
故①正确,③错误;
∵∠ABD=60°,∠ABE=∠DBF,
∴∠EBF=60°.
故②正确;
∵△DEF的周长=DE+DF+EF=AD+EF=4+EF,
∴当EF最小时.∵△DEF的周长最小.
∵∠EBF=60°,BE=BF,∴△BEF是等边三角形,
∴EF=BE,
∴当BE⊥AD时,BE长度最小,即EF长度最小.
∵AB=4,∠A=60°,BE⊥AD,
∴EB=2![]() ,
,
∴△DEF的周长最小值为4+2![]() .
.
故④正确.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校要了解学生每天的课外阅读时间情况,随机调查了部分学生,对学生每天的课外阅读时间x(单位:min)进行分组整理,并绘制了如图所示的不完整的统计图表,根据图中提供的信息,解答下列问题:
(1)本次调查共抽取了________名学生;
(2)统计表中a=________,b=________;
(3)将频数分布直方图补充完整;
(4)若全校共有1200名学生,请估计阅读时间不少于45 min的有多少人.
课外阅读时间x/min
频数/人
百分比
0≤x<15
6
10%
15≤x<30
12
20%
30≤x<45
a
25%
45≤x<60
18
b
60≤x<75
9
15%
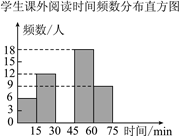
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2﹣2x﹣3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.
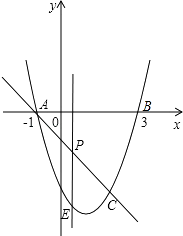
(1)求A、B两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了改善办学条件,计划购置一批电子白板和一批笔记本电脑,经投标,购买1块电子白板比买3台笔记本电脑多3000元,购买4块电子白板和5台笔记本电脑共需80000元.
(1)求购买1块电子白板和一台笔记本电脑各需多少元?
(2)根据该校实际情况,需购买电子白板和笔记本电脑的总数为396,要求购买的总费用不超过2700000元,并购买笔记本电脑的台数不超过购买电子白板数量的3倍,该校有哪几种购买方案?
(3)上面的哪种购买方案最省钱?按最省钱方案购买需要多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=ax+c(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图像可能是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰Rt△ABC中,∠BAC=90°,AB=AC=10,等腰直角三角形ADE绕着点A旋转,∠DAE=90°,AD=AE=6,连接BD、CD、CE,点M、P、N分别为DE、DC、BC的中点,连接MP、PN、MN,则△PMN的面积最大值为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题:
(1)作出△ABC向左平移4个单位长度后得到的△A1B1C1,并写出点C1的坐标;
(2)将△A1B1C1绕原点O逆时针旋转90°得到△A2B2C2,请画出旋转后的△A2B2C2,并写出点C2的坐标.
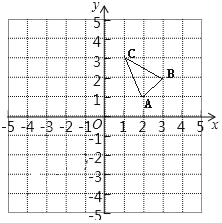
相关试题

