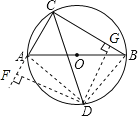
【题目】如图,圆O的直径AB为13cm,弦AC为5cm,∠ACB的平分线圆O于D,则CD长是_______cm

参考答案:
【答案】![]()
【解析】试题分析:首先作DF⊥CA,交CA的延长线于点F,作DG⊥CB于点G,连接DA,DB.由CD平分∠ACB,根据角平分线的性质得出DF=DG,由HL证明△AFD≌△BGD,得出CF的长,又△CDF是等腰直角三角形,从而求出CD的长.
解:作DF⊥CA,垂足F在CA的延长线上,作DG⊥CB于点G,连接DA,DB.
∵CD平分∠ACB,
∴∠ACD=∠BCD
∴DF=DG,![]() ,
,
∴DA=DB.
∵∠AFD=∠BGD=90°,
在Rt△ADF和Rt△BDG,
![]() ,
,
∴Rt△AFD≌Rt△BGD(HL),
∴AF=BG.
同理:Rt△CDF≌Rt△CDG(HL),
∴CF=CG.
∵AB是直径,
∴∠ACB=90°,
∵AC=5cm,AB=13cm,
∴BC=![]() =12(cm),
=12(cm),
∴5+AF=12﹣AF,
∴AF=![]() ,
,
∴CF=![]() ,
,
∵CD平分∠ACB,
∴∠ACD=45°,
∵△CDF是等腰直角三角形,
∴CD=![]() (cm).
(cm).
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求下列各式中
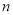 的值:
的值:(1)
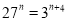 ;(2)
;(2)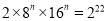 .
.【答案】(1)2 ;(2)3.
【解析】试题分析:(1)、(2)都是把方程两边的底数变为相同的,根据指数相等得到有关n的方程,然后解方程即可得.
试题解析:(1)27n=3n+4,
(33)n=3n+4,
33n=3n+4,
所以,3n=n+4,
n=2;
(2)
 ,
,2×(23)n×(24)n=222,
2×23n×24n=222,
21+3n+4n=222,
所以,1+3n+4n=22,
n=3.
【题型】解答题
【结束】
21【题目】一个多边形的所有内角与它的一个外角之和是2018°,求这个外角的度数和它的边数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠CBA=90°,∠CAB的角平分线AP和∠ACB外角的平分线CF相交于点D,AD交CB于点P,CF交AB的延长线于点F,过点D作DE⊥CF交CB的延长线于点G,交AB的延长线于点E,连接CE并延长交FG于点H,则下列结论:①∠CDA=45°;②AF-CG=CA;③DE=DC;④FH=CD+GH;⑤CF=2CD+EG.其中正确的有( )
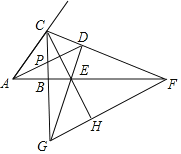
A. ①②④ B. ①②③ C. ①②④⑤ D. ①②③⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列多项式因式分解;
6x3y-12x2y2+6xy3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, ⊙O 的半径是2,直线l与⊙O 相交于A、B 两点,M、N 是⊙O 上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB 面积的最大值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】用一个平面去截①圆锥、②圆柱、③球、④五棱柱,能得到的截面是圆的图形是( )
A.②④B.①②③C.②③④D.①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.x2+x3=2x5B.x2 x3=x6C.(﹣x3)2=﹣x5D.x6÷x3=x3
相关试题

