【题目】已知抛物线经过点A(﹣1,0),B(3,0),C(1,4),与y轴交于点E.
(1)求抛物线的解析式
(2)点F在第三象限的抛物线上,且S△BEF=15,求点F的坐标
(3)点P是x轴上一个动点,过P作直线l∥AE交抛物线于点Q,若以A,P,Q,E为顶点的四边形是平行四边形,请直接写出符合条件的点Q的坐标;如果没有,请通过计算说明理由.
参考答案:
【答案】
(1)
解:设抛物线解析式y=ax2+bx+c,把点A(﹣1,0),B(3,0),C(1,4)代入得:
 ,
,
解得:  ,
,
∴抛物线的解析式是y=﹣x2+2x+3;
(2)
解:设x轴上有一点G,使得S△EGB=15,
∵EO=3,
∴BG=10,
∵BO=3,
∴OG=7,
∴点G坐标是(﹣7,0),
过G作GF∥BE,交第三象限抛物线于点F,
设直线BE的解析式为y=kx+b,
由点B(3,0),点E坐标(0,3)可得y=﹣x﹣3,
∴直线GF解析式为y=﹣x﹣7,
联立抛物线和直线GF的解析式得: ![]() ,
,
解得:x=﹣2,y=﹣5或x=5,y=12,
∵点F在第三象限的抛物线上,
∴点F的坐标是(﹣2,﹣5);
(3)
解:∵直线l∥AC,
∴PQ∥AC且PQ=AC,
∵A(﹣1,0),C(0,3),
∴设点P的坐标为(x,0),
则①若点Q在x轴上方,则点Q的坐标为(x+1,3),
此时,﹣(x+1)2+2(x+1)+3=3,
解得x1=﹣1(舍去),x2=1,
所以,点Q的坐标为(2,3),
②若点Q在x轴下方,则点Q的坐标为(x﹣1,﹣3),
此时,﹣(x﹣1)2+2(x﹣1)+3=﹣3,
整理得,x2﹣4x﹣3=0,
解得x1=2+ ![]() ,x2=2﹣
,x2=2﹣ ![]() ,
,
所以,点Q的坐标为(1+ ![]() ,﹣3)或(1﹣
,﹣3)或(1﹣ ![]() ,﹣3),
,﹣3),
综上所述,点Q的坐标为(2,3)或(1+ ![]() ,﹣3)或(1﹣
,﹣3)或(1﹣ ![]() ,﹣3).
,﹣3).

【解析】(1)设抛物线解析式y=ax2+bx+c,把点A(﹣1,0),B(3,0),C(1,4),分别代入求出a,b,c的值即可求出抛物线的解析式;(2)设x轴上有一点G,使得S△EGB=15,易求点G的坐标,过点G作GF∥BE,交第三象限抛物线于点F,求出直线GF解析式,即可求出点F的坐标(3)分点P在点Q的左边和右边两种情况,根据平行四边形的对边平行且相等,从点A、C的坐标关系,用点P的坐标表示出点Q的坐标,然后把点Q的坐标代入抛物线解析式求解即可.
【考点精析】关于本题考查的确定一次函数的表达式和三角形的面积,需要了解确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;三角形的面积=1/2×底×高才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=65时,y=55;x=75时,y=45.
(1)求一次函数y=kx+b的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,点E在BC上,以CE为直径的⊙O交AB于点F,AO∥EF

(1)求证:AB是⊙O的切线;
(2)如图2,连结CF交AO于点G,交AE于点P,若BE=2,BF=4,求 的值.
的值. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一块正方形和一块等腰直角三角形如图1摆放.
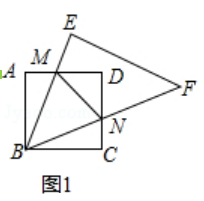
(1)如果把图1中的△BCN绕点B逆时针旋转90°,得到图2,则∠GBM=;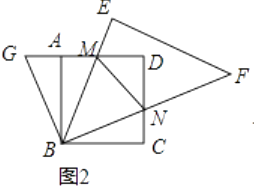
(2)将△BEF绕点B旋转.
①当M,N分别在AD,CD上(不与A,D,C重合)时,线段AM,MN,NC之间有一个不变的相等关系式,请你写出这个关系式:;(不用证明)
②当点M在AD的延长线上,点N在DC的延长线时(如图3),①中的关系式是否仍然成立?若成立,写出你的结论,并说明理由;若不成立,写出你认为成立的结论,并说明理由.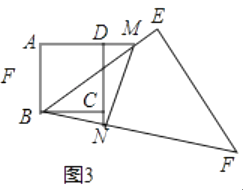
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中既是轴对称图形,又是中心对称图形的是( )
A.
B.
C.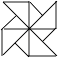
D.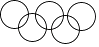
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=20°,则∠B的度数是( )

A.70°
B.65°
C.60°
D.55° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC=10,BC=12,动点P从A点出发,按A→B的方向在AB上移动,动点Q从B点出发,按B→C的方向在BC上移动(当P点到达点B时,P点和Q点停止移动,且两点的移动速度相等),记PA=x,△BPQ的面积为y,则y关于x的函数图象大致是( )

A.
B.
C.
D.
相关试题

