【题目】将一块正方形和一块等腰直角三角形如图1摆放.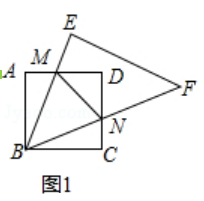
(1)如果把图1中的△BCN绕点B逆时针旋转90°,得到图2,则∠GBM=;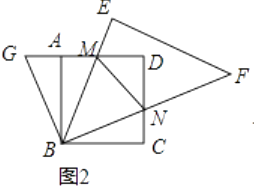
(2)将△BEF绕点B旋转.
①当M,N分别在AD,CD上(不与A,D,C重合)时,线段AM,MN,NC之间有一个不变的相等关系式,请你写出这个关系式:;(不用证明)
②当点M在AD的延长线上,点N在DC的延长线时(如图3),①中的关系式是否仍然成立?若成立,写出你的结论,并说明理由;若不成立,写出你认为成立的结论,并说明理由.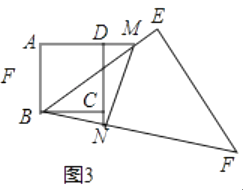
参考答案:
【答案】
(1)45°
(2)MN=AM+CN
【解析】解:(1)在正方形ABCD和等腰直角△BEF中,
∵∠ABC=90°,
∴∠EBF=45°,
∴∠ABM+∠CBN=45°,
由旋转的性质得∠GBA=∠CBN,
∴∠ABM+∠GBA=45°,
即∠GBM=45°,
所以答案是:45°;
⑵①AM+NC=MN;
理由:∵把图1中的△BCN绕点B逆时针旋转90°得到△ABG,
∴∠GAB=∠C=90°,AG=CN,BG=BN,∠ABG=∠CBN,
∴∠GAB+∠DAB=180°,
∴D,A,G三点共线,
∴∠ABM+∠GBA=45°,
∴∠GBM=∠MBN,
在△GBM与△NBM中, 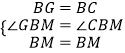 ,
,
∴△GBM≌△NBM,
∴GM=MN,
∵GM=AG+AM=CN+AM,
∴MN=AM+CN;
所以答案是:MN=AM+CN;
②上面的式子不成立,结论是:AM﹣NC=MN,
理由:在AM上截取AG,使得AG=CN,连结BG;
∵四边形ABCD是正方形,
∴AB=BC,∠A=∠BCN=90°,
在△BAG与△BCN中, 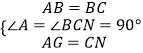 ,
,
∴△BAG≌△BCN,
∴BG=BN,∠ABG=∠NBC,
∴∠MBN=∠MBC+∠CBN=∠MBC+∠ABG=45°=∠GBM,
在△BGM与△BMN中,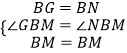 ,
,
∴△BGM≌△BNM,
∴GM=NM,
∴AM﹣CN=MN.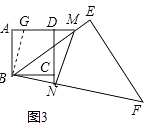
【考点精析】本题主要考查了正方形的性质和旋转的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣3x+k=0有两个实数根x1和x2
(1)求实数k的取值范围;
(2)若|x1﹣x2|=3﹣x1x2时,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=65时,y=55;x=75时,y=45.
(1)求一次函数y=kx+b的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,点E在BC上,以CE为直径的⊙O交AB于点F,AO∥EF

(1)求证:AB是⊙O的切线;
(2)如图2,连结CF交AO于点G,交AE于点P,若BE=2,BF=4,求 的值.
的值. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线经过点A(﹣1,0),B(3,0),C(1,4),与y轴交于点E.
(1)求抛物线的解析式
(2)点F在第三象限的抛物线上,且S△BEF=15,求点F的坐标
(3)点P是x轴上一个动点,过P作直线l∥AE交抛物线于点Q,若以A,P,Q,E为顶点的四边形是平行四边形,请直接写出符合条件的点Q的坐标;如果没有,请通过计算说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中既是轴对称图形,又是中心对称图形的是( )
A.
B.
C.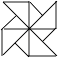
D.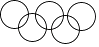
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=20°,则∠B的度数是( )

A.70°
B.65°
C.60°
D.55°
相关试题

