【题目】已知数轴上有A,B,C三点,分别代表﹣30,﹣10,10,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒. 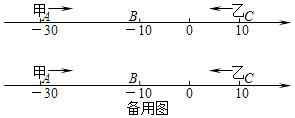
(1)甲,乙在数轴上的哪个点相遇?
(2)多少秒后,甲到A,B,C的距离和为48个单位?
(3)在甲到A,B,C的距离和为48个单位时,若甲调头并保持速度不变,则甲,乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由.
参考答案:
【答案】
(1)解:设x秒后,甲、乙在数轴上相遇.
则4x+6x=40,解得x=4,
﹣30+4×4=﹣14
答:甲,乙在数轴上表示﹣14的点相遇
(2)解:解:能.显然,当甲在点C右侧时,甲到A,B,C的距离和大于40+20=60,
故甲应运动到AB或BC之间.
设y秒后,甲到A,B,C的距离和为48个单位.
当甲在AB之间时:4y+(20﹣4y)+(40﹣4y)=48,
解得y=3;
当甲在BC之间时:4y+(4y﹣20)+(40﹣4y)=48,
解得x=7;
答:3或7秒后,甲到A,B,C的距离和为48个单位
(3)设甲调头z秒后与乙相遇.
若甲从A向右运动3秒时返回,
甲表示的数为:﹣30+4×3﹣4z;乙表示的数为:10﹣6×3﹣6z,
由题意得:﹣30+4×3﹣4z=10﹣6×3﹣6z,
解得z=5.
相遇点表示的数为:﹣30+4×3﹣4×5=﹣38.
若甲从A向右运动7秒时返回,
甲表示的数为:﹣30+4×7﹣4z;乙表示的数为:10﹣6×7﹣6z,
依据题意得:﹣30+4×7﹣4z=10﹣6×7﹣6z,
解得z=﹣15(舍去).
(注:此时甲在表示﹣2的点上,乙在表示﹣32的点上,乙在甲的左侧,甲追及不上乙,因而不可能相遇.)
答:甲从A向右运动3秒时返回,甲,乙能在数轴上相遇,相遇点表示的数为﹣38.
【解析】(1)设x秒后甲与乙相遇,根据甲与乙的路程和为40,可列出方程求解即可;(2)设y秒后甲到A,B,C三点的距离之和为48个单位,分甲应为于AB或BC之间两种情况讨论即可求解:(3)设z秒后甲与乙在数轴上相遇,需要分类讨论:①若甲从A向右运动3秒时返回;②若甲从A向右运动7秒时返回,分别表示出甲、乙表示的数,结合线段间的和差关系列出方程并解答.
【考点精析】关于本题考查的数轴,需要了解数轴是规定了原点、正方向、单位长度的一条直线才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,对角线AC、BD相交于O,EF过点O,且AF⊥BC.
(1)求证:△BFO≌△DEO;
(2)若EF平分∠AEC,试判断四边形AFCE的形状,并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是点是【A,B】的好点.
(1)如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是【A,B】的好点; 又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D【A,B】的好点,但点D【B,A】的好点.(请在横线上填是或不是)知识运用:
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2.数所表示的点是【M,N】的好点;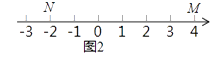
(3)如图3,A、B为数轴上两点,点A所表示的数为﹣20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以4个单位每秒的速度向左运动,到达点A停止.当经过秒时,P、A和B中恰有一个点为其余两点的好点?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y+3与x+2成正比例,且当x=3时,y=7.
(1)写出y与x之间的函数关系式;
(2)当x=﹣1时,求y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市从2017年开始大力发展旅游产业.据统计该市2017年旅游收入约为2亿元,预计2019旅游收入达到2.88亿元,据此估计该市2018年、2019年旅游收入的年平均增长率约为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. 3a2﹣2a2=1B. (﹣a2b3)2=a4b6
C. (﹣a2)3=﹣a5D. a2a3=a6
-
科目: 来源: 题型:
查看答案和解析>>【题目】受益于电子商务发展和法治环境改善等多重因素,快递业务迅猛发展,预计某市2019年快递业务量将达到6.5亿件,数据6.5亿用科学记数法表示为___
相关试题

