【题目】阅读理解:若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是点是【A,B】的好点.
(1)如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是【A,B】的好点; 又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D【A,B】的好点,但点D【B,A】的好点.(请在横线上填是或不是)知识运用: 
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2.数所表示的点是【M,N】的好点; 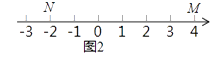
(3)如图3,A、B为数轴上两点,点A所表示的数为﹣20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以4个单位每秒的速度向左运动,到达点A停止.当经过秒时,P、A和B中恰有一个点为其余两点的好点? 
参考答案:
【答案】
(1)不是;是
(2)0
(3)5或10
【解析】解:(1)如图1,∵点D到点A的距离是1,到点B的距离是2, 根据好点的定义得:DB=2DA,那么点D不是【A,B】的好点,但点D是【B,A】的好点;
⑵如图2,4﹣(﹣2)=6,6÷3×2=4,
即距离点M4个单位,距离点N2个单位的点就是所求的好点0;
∴数0所表示的点是【M,N】的好点;
⑶如图3,由题意得:PB=4t,AB=40+20=60,PA=60﹣4t,
点P走完所用的时间为:60÷4=15(秒),
当PB=2PA时,即4t=2(60﹣4t),t=10(秒),
当PA=2PB时,即2×4t=60﹣4t,t=5(秒),
∴当经过5秒或10秒时,P、A和B中恰有一个点为其余两点的好点;
故答案:(1)不是,是;(2)0;(3)5或10.
【考点精析】本题主要考查了数轴和两点间的距离的相关知识点,需要掌握数轴是规定了原点、正方向、单位长度的一条直线;同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一次函数y=(k﹣2)x+1的图象经过一、二、三象限,那么常数k的取值范围是______.
-
科目: 来源: 题型:
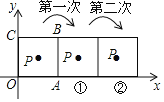
查看答案和解析>>【题目】如图,把正方形铁片OABC置于平面直角坐标系中,顶点A的坐标为(3,0),点P(1,2)在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°,第一次旋转至图①位置,第二次旋转至图②位置…,则正方形铁片连续旋转2017次后,点P的坐标为_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,对角线AC、BD相交于O,EF过点O,且AF⊥BC.
(1)求证:△BFO≌△DEO;
(2)若EF平分∠AEC,试判断四边形AFCE的形状,并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y+3与x+2成正比例,且当x=3时,y=7.
(1)写出y与x之间的函数关系式;
(2)当x=﹣1时,求y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上有A,B,C三点,分别代表﹣30,﹣10,10,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.
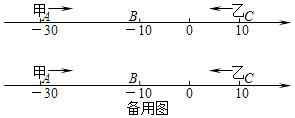
(1)甲,乙在数轴上的哪个点相遇?
(2)多少秒后,甲到A,B,C的距离和为48个单位?
(3)在甲到A,B,C的距离和为48个单位时,若甲调头并保持速度不变,则甲,乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市从2017年开始大力发展旅游产业.据统计该市2017年旅游收入约为2亿元,预计2019旅游收入达到2.88亿元,据此估计该市2018年、2019年旅游收入的年平均增长率约为____.
相关试题

