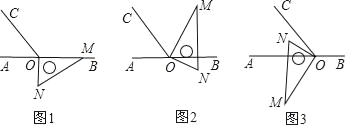
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=112°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,问:射线ON是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O按每秒4°的速度沿逆时针方向旋转至图3,使射线ON恰好平分锐角∠AOC,求此时旋转一共用了多少时间?
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
参考答案:
【答案】(1)平分,理由见解析;(2)此时旋转一共用了59秒;(3)∠AOM﹣∠NOC=22°,理由见解析
【解析】
(1)延长NO到点D,先得出∠MOB为直角,再利用∠MOB和∠MOC,可分别求出∠NOB和∠COD的大小,最后求出∠AOD的大小,得到平分;
(2)先求出旋转的角度,然后用角度除速度即可;
(3)∠AOM和∠NOC都用含∠AON的式子表示出来,代入抵消可得结果
解:(1)平分,理由:延长NO到D,
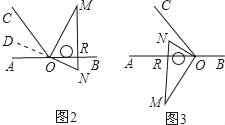
∵∠MON=90°∴∠MOD=90°
∴∠MOB+∠NOB=90°,
∠MOC+∠COD=90°,
∵∠MOB=∠MOC=56° ∴∠NOB=∠COD=34°,
∵∠AOD=180°-∠BOC-∠COD=34°,
∴∠COD=∠AOD, ∴直线NO平分∠AOC;
(2)如图3,当NO平分∠AOC时,∠NOA=34°,
∴∠AOM=56°, 即逆时针旋转的角度为:180°+56°=236°,
由题意得,236÷4=59(秒)
答:此时旋转一共用了59秒
(3)∠AOM﹣∠NOC=22°,
理由:∵∠AOM=90°﹣∠AON ∠NOC=68°﹣∠AON,
∴∠AOM﹣∠NOC
=(90°﹣∠AON)﹣(68°﹣∠AON)
=22°.
-
科目: 来源: 题型:
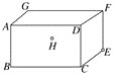
查看答案和解析>>【题目】长方体敞口玻璃罐,长、宽、高分别为16 cm、6 cm和6 cm,在罐内点E处有一小块饼干碎末,此时一只蚂蚁正好在罐外壁,在长方形ABCD中心的正上方2 cm处,则蚂蚁到达饼干的最短距离是多少cm.( )
A. 7
 B.
B. 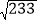
C. 24D.
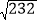
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个长为4,宽为3,高为12矩形牛奶盒,从上底一角的小圆孔插入一根到达底部的直吸管,吸管在盒内部分a的长度范围是(牛奶盒的厚度、小圆孔的大小及吸管的粗细均忽略不计)( )

A. 5≤a≤12B. 12≤a≤3
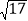
C. 12≤a≤4
 D. 12≤a≤13
D. 12≤a≤13 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.求证:AC平分∠DAB.
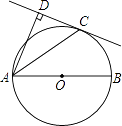
-
科目: 来源: 题型:
查看答案和解析>>【题目】按要求完成下列证明:
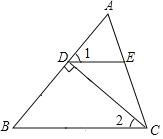
已知:如图,在△ABC中,CD⊥AB于点D,E是AC上一点,且∠1+∠2=90°.
求证:DE∥BC.
证明:∵CD⊥AB(已知),
∴∠1+ =90°( ).
∵∠1+∠2=90°(已知),
∴ =∠2( ).
∴DE∥BC( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,BE与CD相交于点G,且OE=OD,则AP的长为______.

-
科目: 来源: 题型:
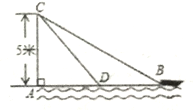
查看答案和解析>>【题目】在杭州西湖风景游船处,如图,在离水面高度为5m的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13m,此人以0.5m/s的速度收绳.10s后船移动到点D的位置,问船向岸边移动了多少m?(假设绳子是直的,结果保留根号)
相关试题

