【题目】为了庆祝新中国成立70周年,某校组织八年级全体学生参加“恰同学少年,忆峥嵘岁月”新中国成立70周年知识竞赛活动.将随机抽取的部分学生成绩进行整理后分成5组,50~60分(![]() )的小组称为“学童”组,60~70分(
)的小组称为“学童”组,60~70分(![]() )的小组称为“秀才”组,70~80分(
)的小组称为“秀才”组,70~80分(![]() )的小组称为“举人”组,80~90分(
)的小组称为“举人”组,80~90分(![]() )的小组称为“进士”组,90~100分(
)的小组称为“进士”组,90~100分(![]() )的小组称为“翰林”组,并绘制了不完整的频数分布直方图如下,请结合提供的信息解答下列问题:
)的小组称为“翰林”组,并绘制了不完整的频数分布直方图如下,请结合提供的信息解答下列问题:
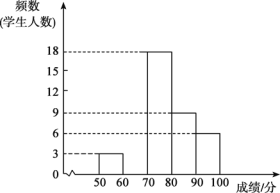
(1)若“翰林”组成绩的频率是12.5%,请补全频数分布直方图;
(2)在此次比赛中,抽取学生的成绩的中位数在 组;
(3)学校决定对成绩在70~100分(![]() )的学生进行奖励,若八年级共有336名学生,请通过计算说明,大约有多少名学生获奖?
)的学生进行奖励,若八年级共有336名学生,请通过计算说明,大约有多少名学生获奖?
参考答案:
【答案】(1)详见解析;(2)70~80或“举人”;(3)231.
【解析】
(1)先根据90~100分的人数及其所占百分比求得总人数,再由各组人数之和等于总人数求得60~70分的人数.从而补全图形;
(2)根据中位数的定义求解可得;
(3)利用样本估计总体的思想求解可得.
解:(1)∵被调查的总人数为6÷12.5%=48(人),
∴60~70分的人数为48-(3+18+9+6)=12(人),
补全频数分布直方图如下:
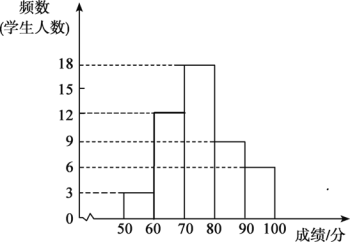
(2)因为中位数是第24、25个数据的平均数,而第24、25个数据都落在70~80分这一组,
所以在此次比赛中,抽取学生的成绩的中位数在70~80或“举人”组,
故答案为:70~80或“举人”;
(3)![]() .
.
答:大约有231名学生获奖.
故答案为:(1)详见解析;(2)70~80或“举人”;(3)231.
-
科目: 来源: 题型:
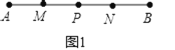
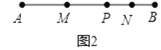
查看答案和解析>>【题目】如图,点P是线段AB上的一点,点M、N分别是线段AP、PB的中点.
(1)如图1,若点P是线段AB的中点,且MP=4cm,求线段AB的长;
(2)如图2,若点P是线段AB上的任一点,且AB=12cm,求线段MN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形ABCD是平行四边形,CE∥BD交AD的延长线于点E,CE=AC.
(1)求证:四边形ABCD是矩形;
(2)若AB=4,AD=3,求四边形BCED的周长.

-
科目: 来源: 题型:
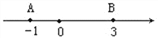
查看答案和解析>>【题目】已知数轴上两点A、B对应的数分别为—1,3,点P为数轴上一动点,其对应的数为x。
⑴若点P到点A、点B的距离相等,求点P对应的数;
⑵数轴上是否存在点P,使点P到点A、点B的距离之和为5?若存在,请求出x的值。若不存在,请说明理由?
⑶当点P以每分钟一个单位长度的速度从O点向左运动时,点A以每分钟5个单位长度向左运动,点B以每分钟20个单位长度向左运动,问它们同时出发,几分钟后点P到点A、点B的距离相等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学七年级A班有50人,某次活动中分为三组,第一组有(3a+4b+2)人,第二组比第一组的一半多6人.
(1)求第三组的人数;(用含a,b的整式表示)
(2)试判断当a=1,b=2时,是否满足题意.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市居民生活用水实行“阶梯水价”收费,具体收费标准见下表:
每户每月用水量
水的价格(单位:元/吨)
不超过20吨的部分
1.6
超过20吨且不超过30吨的部分
2.4
超过30吨的部分
3.3
例:甲用户1月份用水25吨,应缴水费
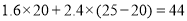 (元).
(元).(1)若乙用户1月份用水10吨,则应缴水费________元;
(2)若丙用户1月份应缴水费62.6元,则用水________吨;.
(3)若丁用户1、2月份共用水60吨(1月份用水量超过了2月份),设2月份用水
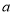 吨,求丁用户1、2月份各应缴水费多少元.(用含
吨,求丁用户1、2月份各应缴水费多少元.(用含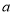 的代数式表示)
的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】 要比较a与b的大小,可以先求a与b的差,再看这个差是正数、负数还是零.由此可见,要判断两个式子值的大小,只要考虑它们的差就可以了.
已知A=16a2+a+15 , B=4a2+
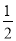 a+7 , C=a2+
a+7 , C=a2+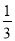 a+4.
a+4.请你按照上述文字提供的信息:(1)试比较A与2B的大小; (2)试比较2B与3C的大小.
相关试题

