【题目】永辉超市进行有奖促销活动.活动规则:购买500元商品就可以获得一次转转盘的机会(转盘分为5个扇形区域,分别是特等奖、一等奖、二等奖、三等奖、不获奖),转盘指针停在哪个获奖区域就可以获得该区域相应等级奖品一件.商场工作人员在制作转盘时,将获奖扇形区域圆心角分配如下表:
奖次 | 特等奖 | 一等奖 | 二等奖 | 三等奖 |
圆心角 |
|
|
|
|
促销公告
凡购买我商场商品均有可能获得下列大奖:
特等奖:彩电一台 一等奖:自行车一辆 二等奖:圆珠笔一支 三等奖:卡通画一张
(1)获得圆珠笔的概率是多少?
(2)不获奖的概率是多少?
(3)如果不用转盘,请设计一种等效试验方案.(要求写清楚替代工具和实验规则)
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)可采用“抓阄”或“抽签”等方法替代
(3)可采用“抓阄”或“抽签”等方法替代
【解析】
(1根据圆珠笔所占的圆心角度数计算即可.
(2)首先计算三等奖以上包括三等奖的圆心角的和,再计算不获奖圆心角的度数,进而计算不获奖的概率.
(3)采用最常规的“抓阄”或“抽签”等方法替代.按住转盘设置数量即可.
(1)获得圆珠笔的概率为:![]() .
.
(2)不获奖的圆心角的度数为:![]()
不获奖的概率为:![]() .
.
(3)可采用“抓阄”或“抽签”等方法替代.
在一个不透明的箱子里放进360个除标号不同外,其他均一样的兵乓球,其中1个标“特”、36个标“1”、53个标“2”、150个标“3”、其余不标数字,摸出标有哪个奖次的乒乓球,则获相应等级的奖品.
-
科目: 来源: 题型:
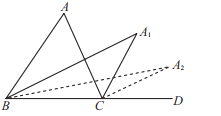
查看答案和解析>>【题目】如图,在
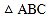 中,
中,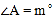 ,
,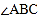 和
和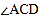 的平分线交于点
的平分线交于点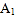 ,得
,得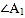 ;
;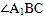 和
和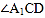 的平分线交于点
的平分线交于点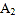 ,得
,得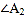 ;…;
;…;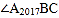 和
和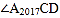 的平分线交于点
的平分线交于点 ,则
,则 =___________.
=___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,O是坐标原点,一次函数y=kx+b的图象与x轴交于点A(﹣3,0),与y轴交于点B,且与正比例函数y=
 x的图象的交点为C(m,4).
x的图象的交点为C(m,4).
(1)求一次函数y=kx+b的解析式;
(2)D是平面内一点,以O、C、D、B四点为顶点的四边形是平行四边形,直接写出点D的坐标.(不必写出推理过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,函数y=ax2+bx与y=bx+a的图像可能是( )
A.
 B.
B. 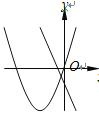 C.
C. 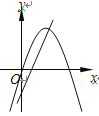 D.
D. 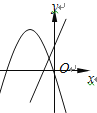
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A是∠MON边OM上一点,AE∥ON.

(1)在图中作∠MON的角平分线OB(要求用尺规),交AE于点B;过点A画OB的垂线,垂足为点D,交ON于点C,连接CB,将图形补充完整.
(2)判断四边形OABC的形状,并证明你的结论.
解:四边形OABC是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在
 中,
中, ,
, ,分别过
,分别过 、
、 两点作过点
两点作过点 的直线
的直线 的垂线,垂足为
的垂线,垂足为 、
、 ;
;
(1)如图1,当
 、
、 两点在直线
两点在直线 的同侧时,猜想,
的同侧时,猜想, 、
、 、
、 三条线段有怎样的数量关系?并说明理由.
三条线段有怎样的数量关系?并说明理由.(2)如图2,当
 、
、 两点在直线
两点在直线 的两侧时,
的两侧时, 、
、 、
、 三条线段有怎样的数量关系?并说明理由.
三条线段有怎样的数量关系?并说明理由.(3)如图3,
 ,
, ,
, .点
.点 从
从 点出发沿
点出发沿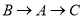 路径向终点
路径向终点 运动;点
运动;点 从
从 点出发沿
点出发沿 路径向终点
路径向终点 运动.点
运动.点 和
和 分别以每秒2和3个单位的速度同时开始运动,只要有一点到达相应的终点时两点同时停止运动;在运动过程中,分别过
分别以每秒2和3个单位的速度同时开始运动,只要有一点到达相应的终点时两点同时停止运动;在运动过程中,分别过 和
和 作
作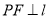 于
于 ,
, 于
于 .问:点
.问:点 运动多少秒时,
运动多少秒时, 与
与 全等?(直接写出结果即可)
全等?(直接写出结果即可) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知边长为3的正方形的对角线长
 为
为 ,给出下列关于
,给出下列关于 的四个结论:①
的四个结论:① 是无理数;②
是无理数;② 可以用数轴上的点表示;③
可以用数轴上的点表示;③ ;④
;④ 是18的算术平方根.其中正确的是( )
是18的算术平方根.其中正确的是( )A. ①④B. ②③C. ①②④D. ①③④
相关试题

