搜索
【题目】如图，直线AB，CD相交于点O，OE平分∠AOC，∠AOD比∠AOE大75°，求∠AOD的度数．
参考答案：
【答案】110°.
【解析】两直线相交，对顶角相等，直线AB，CD相交于点O，则∠AOD与∠AOC互为邻补角，即∠AOD＋∠AOC＝180°，又因为OE平分∠AOC，所以2∠AOE＝∠AOC，所以∠AOE＝
（180°∠AOD），再根据∠AOD比∠AOE大75°，可求出∠AOD的度数．
∵AB，CD相交于点O，
∴∠AOD＋∠AOC＝180°，
又∵OE平分∠AOC，
∴2∠AOE＝∠AOC，
∴∠AOE＝（180°∠AOD），
∵∠AOD∠AOE＝75°，
∴∠AOD（180°∠AOD）＝75°，
∴
∠AOD＝165°，
∴∠AOD＝110°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD外取一点E，连接AE、BE、DE．过点A作AE的垂线交DE于点P．若AE=AP=1，PB=
．下列结论：①△APD≌△AEB；②点B到直线AE的距离为
；③EB⊥ED；④S△APD+S△APB=1+
；⑤S正方形ABCD=4+．其中正确结论的序号是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在四边形ABCD中，∠DAB被对角线AC平分，且AC2=ABAD．我们称该四边形为“可分四边形”，∠DAB称为“可分角”．
（1）如图2，在四边形ABCD中，∠DAB=60°，AC平分∠DAB，且∠BCD=150°，求证：四边形ABCD为“可分四边形”；
（2）如图3，四边形ABCD为“可分四边形”，∠DAB为“可分角”，如果∠DCB=∠DAB，则求∠DAB的度数；
（3）现有四边形ABCD为“可分四边形”，∠DAB为“可分角”，且AC=4，则△DAB的最大面积等于 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知
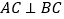于点C，AC=4，BC=
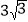，将线段AC绕点A按逆时针方向旋转
，得到线段AD，连接DC，DB，则线段DB的长为__________。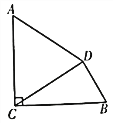
-
科目： 来源： 题型：
查看答案和解析>>【题目】某科技有限公司准备购进A和B两种机器人来搬运化工材料，已知购进A种机器人2个和B种机器人3个共需16万元，购进A种机器人3个和B种机器人2个共需14万元，请解答下列问题：
（1）求A、B两种机器人每个的进价；
（2）已知该公司购买B种机器人的个数比购买A种机器人的个数的2倍多4个，如果需要购买A、B两种机器人的总个数不少于28个，且该公司购买的A、B两种机器人的总费用不超过106万元，那么该公司有哪几种购买方案？
-
科目： 来源： 题型：
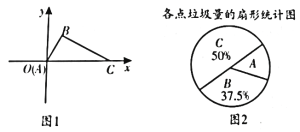
查看答案和解析>>【题目】2017年4月20日，成都举行了“建城市森林，享低碳生活”的垃圾分类推进工作启动仪式，在成都设置有专门的垃圾存放点，做到日产日清。在平面直角坐标系中xOy中,A,B,C三个垃圾存放点的位置如图1所示，点A在原点，
，
.某同学利用周末时间调查了这三个存放点的垃圾量，并绘制了如下尚不完整的扇形统计图（如图2）。（1）若C处的垃圾存放量为320千克，求A处的垃圾存放量。
（2）现需要A，C两处的垃圾分别沿道路AB，CB都运到B处，若点B的横坐标为50，平面直角坐标系中一个单位长度所表示的实际距离是1米，每运送1千克垃圾1米的费用为0.005元，求本次运送垃圾的总费用。（结果保留整数，参考数据：
）
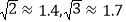相关试题
