【题目】如图1,以边长为8的正方形纸片ABCD的边AB为直径作⊙O,交对角线AC于点E. 
(1)线段AE=;
(2)如图2,以点A为端点作∠DAM=30°,交CD于点M,沿AM将四边形ABCM剪掉,使Rt△ADM绕点A逆时针旋转(如图3),设旋转角为α(0°<α<150°),旋转过程中AD与⊙O交于点F. 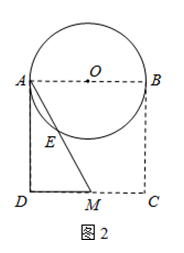
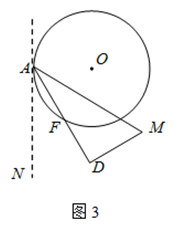
①当α=30°时,请求出线段AF的长;
②当α=60°时,求出线段AF的长;判断此时DM与⊙O的位置关系,并说明理由;
③当α= ![]() 时,DM与⊙O相切.
时,DM与⊙O相切.
参考答案:
【答案】
(1)4 ![]()
(2)解:①连接OA、OF,
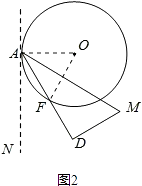
由题意得,∠NAD=30°,∠DAM=30°,
故可得∠OAM=30°,∠DAM=30°,
则∠OAF=60°,
又∵OA=OF,
∴△OAF是等边三角形,
∵OA=4,
∴AF=OA=4;
②连接B'F,此时∠NAD=60°,
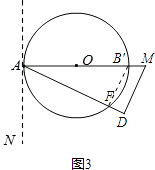
∵AB'=8,∠DAM=30°,
∴AF=AB'cos∠DAM=8× ![]() =4
=4 ![]() ;
;
此时DM与⊙O的位置关系是相离
③ 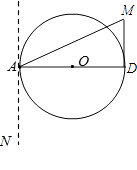
∵AD=8,直径的长度相等,
∴当DM与⊙O相切时,点D在⊙O上,
故此时可得α=∠NAD=90°.
【解析】解:(1)连接BE, 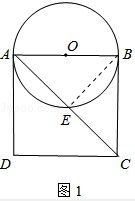
∵AC是正方形ABCD的对角线,
∴∠BAC=45°,
∴△AEB是等腰直角三角形,
又∵AB=8,
∴AE=4 ![]() ;
;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是( )

A.∠AOC=40° B.∠COE=130° C.∠EOD=40° D.∠BOE=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠CAB=90°,AD⊥BC于点D,点E为AB的中点,EC与AD交于点G,点F在BC上.
(1)如图1,AC:AB=1:2,EF⊥CB,求证:EF=CD.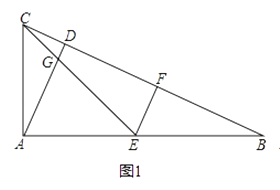
(2)如图2,AC:AB=1: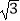 ,EF⊥CE,求EF:EG的值.
,EF⊥CE,求EF:EG的值. 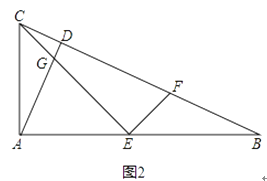
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在7×7网格中,每个小正方形的边长都为1.
(1)建立适当的平面直角坐标系后,若点A(3,4)、C(4,2),则点B的坐标为 ;
(2)图中格点△ABC的面积为 ;
(3)判断格点△ABC的形状,并说明理由.
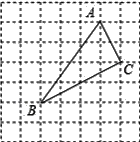
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线AB∥DF,∠D+∠B=180°,

(1)求证:DE∥BC;
(2)如果∠AMD=75°,求∠AGC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1(注:与图2完全相同),二次函数y=
 x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.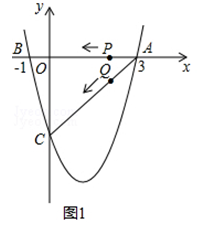
(1)求该二次函数的解析式;
(2)设该抛物线的顶点为D,求△ACD的面积(请在图1中探索);
(3)若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标(请在图2中探索).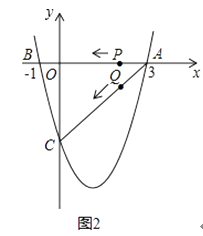
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点,若AB=17,BD=12,
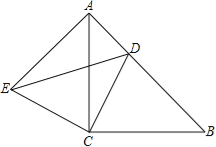
(1)求证:△BCD≌△ACE;
(2)求DE的长度.
相关试题

