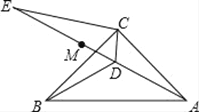
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,且BD=AD.
(1)求证:CD⊥AB;
(2)∠CAD=15°,E为AD延长线上的一点,且CE=CA.
①求证:DE平分∠BDC;
②若点M在DE上,且DC=DM,请判断ME、BD的数量关系,并给出证明;
③若N为直线AE上一点,且△CEN为等腰三角形,直接写出∠CNE的度数.
参考答案:
【答案】(1)详见解析;(2)①详见解析;②:ME=BD,证明详见解析;③∠CNE的度数为7.5°、15°、82.5°、150°.
【解析】
(1)根据中垂线的判定定理“与一条线段两个端点距离相等的点,在这条线段的垂直平分线上”可得出结论.
(2)①由∠CAD=15°,BD=AD与直角等腰三角形的性质可知,∠DBA=∠DAB=30°,则可得∠BDE=30°+30°=60°,又根据SSS可证△ADC≌△BDC,则∠ACD=∠BCD=45°,可知∠CDE=∠ACD+∠CAD=45°+15°=60°,故DE平分∠BDC.
②连接MC,由DC=DM,∠CDE=60°,可知△MCD为等边三角形,∠ECM=∠CMD-∠CAD=45°则根据SAS可证△BDC≌△EMC,得出结论ME=BD.
③根据题意可知,分类:当EN=EC时;当EN=CN时;当CE=CN时三种情况求出∠CNE的度数.
(1)证明:∵CB=CA,DB=DA,
∴CD垂直平分线段AB,
∴CD⊥AB,
故答案为:CD⊥AB.
(2)①证明:∵AC=BC,
∴∠CBA=∠CAB,
又∵∠ACB=90°,
∴∠CBA=∠CAB=45°,
又∵在△ADC和△BDC中,
 ,
,
∴△ADC≌△BDC(SSS),
∴∠CAD=∠CBD=15°,
∴∠DBA=∠DAB=30°,
∴∠BDE=30°+30°=60°,
∵∠ACB=90°,∠ACD=∠BCD,
∴∠ACD=∠BCD=45°,
∴∠CDE=∠ACD+∠CAD=45°+15°=60°,
∵∠CDE=∠BDE=60°,
∴DE平分∠BDC;
故答案为:DE平分∠BDC.
②结论:ME=BD,
理由:连接MC,

∵DC=DM,∠CDE=60°,
∴△MCD为等边三角形,
∴CM=CD,∠CMD=60°,
又∵EC=CA,∠CAD=15°,
∴∠ECM=∠CMD-∠CAD=45°,
在△BDC和△EMC中,
 ,
,
∴△BDC≌△EMC(SAS),
∴ME=BD,
故答案为:ME=BD.
③当EN=EC时,∠ENC=7.5°或82.5°;
当EN=CN时,∠ENC=150°;
当CE=CN时,∠CNE=15°,
故答案为:∠CNE的度数为7.5°、15°、82.5°、150°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小李从西安通过某快递公司给在南昌的外婆寄一盒樱桃,快递时,他了解到这个公司除收取每次6元的包装费外,樱桃不超过1kg收费22元,超过1kg,则超出部分按每千克10元加收费用.设该公司从西安到南昌快递樱桃的费用为y(元),所寄樱桃为x(kg).
(1)求y与x之间的函数关系式;
(2)已知小李给外婆快寄了2.5kg樱桃,请你求出这次快寄的费用是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)2(x﹣3)=3x(x﹣3);
(2)x2﹣2x=2x+1. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:有一个直角三角形ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到离A的距离等于___________时,ΔABC和ΔPQA全等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠ABC=72°.
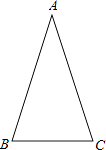
(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);
(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数. -
科目: 来源: 题型:
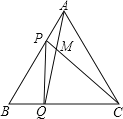
查看答案和解析>>【题目】点P、Q分别是边长为4cm的等边
 的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都是
的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都是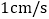 ,设运动时间为t秒.
,设运动时间为t秒.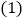 连接AQ、CP交于点M,则在P、Q运动的过程中,
连接AQ、CP交于点M,则在P、Q运动的过程中,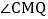 变化吗:若变化,则说明理由,若不变,则求出它的度数;
变化吗:若变化,则说明理由,若不变,则求出它的度数;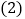 连接PQ,
连接PQ, 当
当 秒时,判断
秒时,判断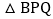 的形状,并说明理由;
的形状,并说明理由; 当
当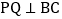 时,则
时,则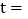 ______秒
______秒 直接写出结果
直接写出结果
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.求证:

(1)BC=AD;
(2)△OAB是等腰三角形.
相关试题

