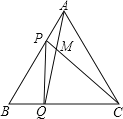
【题目】点P、Q分别是边长为4cm的等边![]() 的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都是
的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都是![]() ,设运动时间为t秒.
,设运动时间为t秒.
![]() 连接AQ、CP交于点M,则在P、Q运动的过程中,
连接AQ、CP交于点M,则在P、Q运动的过程中,![]() 变化吗:若变化,则说明理由,若不变,则求出它的度数;
变化吗:若变化,则说明理由,若不变,则求出它的度数;
![]() 连接PQ,
连接PQ,
![]() 当
当![]() 秒时,判断
秒时,判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 当
当![]() 时,则
时,则![]() ______秒
______秒![]() 直接写出结果
直接写出结果![]()
参考答案:
【答案】(1)在P、Q运动的过程中,∠CMQ不变,∠CMQ=60°;(2)①△BPQ是等边三角形;②![]() .
.
【解析】
(1)先证明△ABQ≌△CAP,得到∠BAQ=∠ACP,根据∠BAQ+∠QAC=60°,然后利用三角形外角的性质即可得出结论;
(2)①当t=2秒时,AP=BQ=2,PB=4﹣2=2,可知△BPQ是等边三角形;
②当PQ⊥BC时,∠B=60°,根据直角三角形30°所对直角边等于斜边一半的性质列等量关系,即可求出时间t.
(1)∵△ABC为等边三角形,
∴AB=AC,∠B=∠PAC=60°,
∵点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,
∴AP=BQ,
在△APC和△BQA中
 ,
,
∴△APC≌△BQA(SAS),
∴∠BAQ=∠ACP,
∴∠CMQ=∠CAQ+∠ACP=∠BAQ+∠CAQ=∠BAC=60°,
∴在P、Q运动的过程中,∠CMQ不变,∠CMQ=60°;
故答案为:在P、Q运动的过程中,∠CMQ不变,∠CMQ=60°.
(2)①∵运动时间为ts,则AP=BQ=t,
∴PB=4﹣t,
当t=2秒时,AP=BQ=2,PB=4﹣2=2,∴AP=BQ=PB,
∴△BPQ是等边三角形;
故答案为:△BPQ是等边三角形.
②∵运动时间为ts,则AP=BQ=t,∴PB=4﹣t,
∵PQ⊥BC,∴∠PQB=90°,
∵∠B=60°,∴PB=2BQ,
∴4﹣t=2t,解得t=![]() ,
,
故答案为:t=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:有一个直角三角形ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到离A的距离等于___________时,ΔABC和ΔPQA全等.

-
科目: 来源: 题型:
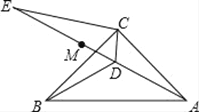
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,且BD=AD.
(1)求证:CD⊥AB;
(2)∠CAD=15°,E为AD延长线上的一点,且CE=CA.
①求证:DE平分∠BDC;
②若点M在DE上,且DC=DM,请判断ME、BD的数量关系,并给出证明;
③若N为直线AE上一点,且△CEN为等腰三角形,直接写出∠CNE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠ABC=72°.
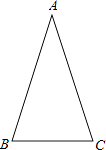
(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);
(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.求证:

(1)BC=AD;
(2)△OAB是等腰三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,路灯下一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN.

(1)指定路灯的位置(用点P表示);
(2)在图中画出表示大树高的线段;
(3)若小明的眼睛近似地看成是点D,试画图分析小明能否看见大树. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN.

(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
相关试题

