【题目】解方程:
(1)2(x﹣3)=3x(x﹣3);
(2)x2﹣2x=2x+1.
参考答案:
【答案】
(1)
解:2(x﹣3)=3x(x﹣3)
移项,得2(x﹣3)﹣3x(x﹣3)=0
整理,得(x﹣3)(2﹣3x)=0
∴x﹣3=0或2﹣3x=0
解得:x1=3,x2= ![]()
(2)
解:原方程化为:x2﹣4x=1
配方,得x2﹣4x+4=1+4
整理,得(x﹣2)2=5
∴x﹣2= ![]() ,
,
即x1=2 ![]() ,x2=2
,x2=2 ![]()
【解析】(1)运用运用因式分解法解一元二次方程;(2)运用配方法解一元二次方程.
【考点精析】掌握配方法和因式分解法是解答本题的根本,需要知道左未右已先分离,二系化“1”是其次.一系折半再平方,两边同加没问题.左边分解右合并,直接开方去解题;已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
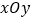 中,过点
中,过点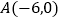 的直线
的直线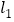 与直线
与直线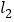 ;
;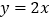 相交于点
相交于点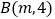 .
.(
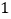 )求直线
)求直线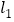 的表达式.
的表达式.(
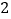 )过动点
)过动点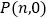 且垂于
且垂于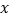 轴的直线与
轴的直线与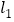 、
、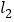 的交点分别为
的交点分别为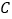 ,
,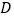 ,当点
,当点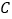 位于点
位于点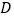 上方时,写出
上方时,写出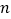 的取值范围.
的取值范围.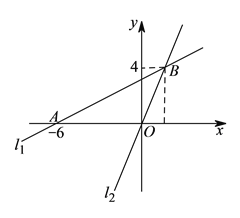
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长12的正方形ABCD中,有一个小正方形EFGH,其中E,F,G分别在AB,BC,FD上.若BF=3,则小正方形的边长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】小李从西安通过某快递公司给在南昌的外婆寄一盒樱桃,快递时,他了解到这个公司除收取每次6元的包装费外,樱桃不超过1kg收费22元,超过1kg,则超出部分按每千克10元加收费用.设该公司从西安到南昌快递樱桃的费用为y(元),所寄樱桃为x(kg).
(1)求y与x之间的函数关系式;
(2)已知小李给外婆快寄了2.5kg樱桃,请你求出这次快寄的费用是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:有一个直角三角形ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到离A的距离等于___________时,ΔABC和ΔPQA全等.

-
科目: 来源: 题型:
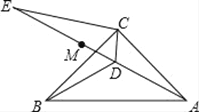
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,且BD=AD.
(1)求证:CD⊥AB;
(2)∠CAD=15°,E为AD延长线上的一点,且CE=CA.
①求证:DE平分∠BDC;
②若点M在DE上,且DC=DM,请判断ME、BD的数量关系,并给出证明;
③若N为直线AE上一点,且△CEN为等腰三角形,直接写出∠CNE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠ABC=72°.
(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);
(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.
相关试题

