【题目】将连续的奇数1,3,5,7,9,…,排成如图7所示的数阵.
(1)十字框中的五个数的和与中间数15有什么关系?
(2)设中间数为![]() ,用式子表示十字框中五个数之和;
,用式子表示十字框中五个数之和;
(3)若将十字框中上下左右移动,可框住另外五个数,这五个数的和还有这种规律吗?
(4)十字框中五个数之和能等于2005吗?若能,请写出这五个数;若不能,说明理由.

参考答案:
【答案】(1)十字框中的五个数的和是中间数15的5倍;(2)5a;(3)有这种规律;(4)但是401在左边界,所以不能框出这5个数.
【解析】
(1)先求出这5个数的和,用这个和去除以中间的这个数15就可以得出结论;
(2)由左右相邻两个奇数之间相差2,上下相邻两个奇数之间相差10,就可以分别表示出这5个数,进而得出结论;
(3)同样设中间数为b,就可以表示出这5个数的和,得出结论与(1)一样;
(4)设中间的一个数为x,建立方程求出x的值就可以得出结论.
(1)由题意,得
5+13+15+17+25=75.
75÷15=5.
∴十字框中的五个数的和是中间数15的5倍;
(2)设中间数为a,则其余的4个数分别为a2,a+2,a10,a+10,由题意,得
a+a2+a+2+a10+a+10=5a.
答:5个数之和为5a;
(3)设设中间数为b,则其余的4个数分别为b2,b+2,b10,b+10,由题意,得
∵b+b2+b+2+b10+b+10=5b,
∴这五个数的和还是中间这个数的5倍;
(4)设中间的一个数为x,则其余的4个数分别为x2,x+2,x10,x+10,由题意,得
x+x2+x+2+x10+x+10=2005,
解得:x=401.
∵401在最左边,
∴不存在十字框中五数之和等于2005.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017山东省菏泽市,第20题,7分)如图,一次函数y=kx+b与反比例函数
 的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.
的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是由四条曲线围成的广告标志,建立平面直角坐标系,双曲线对应的函数表达式分别为y=-
 ,y=
,y= .现用四根钢条固定这四条曲线,这种钢条加工成长方形产品按面积计算,每单位面积25元,请你帮助工人师傅计算一下,所需钢条一共花多少钱?
.现用四根钢条固定这四条曲线,这种钢条加工成长方形产品按面积计算,每单位面积25元,请你帮助工人师傅计算一下,所需钢条一共花多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数图象如图所示,根据图象可得:

(1)抛物线顶点坐标;
(2)对称轴为
(3)当x=时,y有最大值是;
(4)当时,y随着x得增大而增大.
(5)当时,y>0. -
科目: 来源: 题型:
查看答案和解析>>【题目】(中考·安徽)如图,已知反比例函数y=
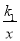 与一次函数y=k2x+b的图象交于A(1,8),B(-4,m).
与一次函数y=k2x+b的图象交于A(1,8),B(-4,m).
(1)求k1,k2,b的值;
(2)求△AOB的面积;
(3)若M(x1,y1),N(x2,y2)是反比例函数y=
 的图象上的两点,且x1<x2,y1<y2,指出点M,N位于哪个象限,并简要说明理由.
的图象上的两点,且x1<x2,y1<y2,指出点M,N位于哪个象限,并简要说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABOD的顶点A是函数y=-x-(k+1)的图象与函数y=
 在第二象限的图象的交点,B,D两点在坐标轴上,且长方形ABOD的面积为3.
在第二象限的图象的交点,B,D两点在坐标轴上,且长方形ABOD的面积为3.(1)求两函数的表达式;
(2)求两函数图象的交点A,C的坐标;
(3)若点P是y轴上一动点,且S△APC=5,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是函数y=
 与函数y=
与函数y= 在第一象限内的图象,点P是y=
在第一象限内的图象,点P是y= 的图象上一动点,PA⊥x轴于点A,交y=
的图象上一动点,PA⊥x轴于点A,交y= 的图象于点C,PB⊥y轴于点B,交y=
的图象于点C,PB⊥y轴于点B,交y= 的图象于点D.
的图象于点D.(1)求证:D是BP的中点;
(2)求四边形ODPC的面积.

相关试题

