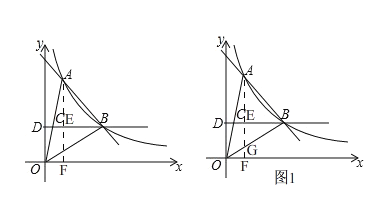
【题目】(2017山东省菏泽市,第20题,7分)如图,一次函数y=kx+b与反比例函数![]() 的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.
的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积.

参考答案:
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)先利用待定系数法求出反比例函数解析式,进而确定出点A的坐标,再用待定系数法求出一次函数解析式;
(2)先求出OB的解析式,进而求出AG,用三角形的面积公式即可得出结论.
试题解析:(1)如图,过点A作AF⊥x轴交BD于E,∵点B(3,2)在反比例函数![]() 的图象上,∴a=3×2=6,∴反比例函数的表达式为
的图象上,∴a=3×2=6,∴反比例函数的表达式为![]() ,∵B(3,2),∴EF=2,∵BD⊥y轴,OC=CA,∴AE=EF=
,∵B(3,2),∴EF=2,∵BD⊥y轴,OC=CA,∴AE=EF=![]() AF,∴AF=4,∴点A的纵坐标为4,∵点A在反比例函数
AF,∴AF=4,∴点A的纵坐标为4,∵点A在反比例函数![]() 图象上,∴A(
图象上,∴A(![]() ,4),∴
,4),∴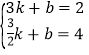 ,∴
,∴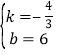 ,∴一次函数的表达式为
,∴一次函数的表达式为![]() ;
;
(2)如图1,过点A作AF⊥x轴于F交OB于G,∵B(3,2),∴直线OB的解析式为y=![]() ,∴G(
,∴G(![]() ,1),∵A(
,1),∵A(![]() ,4),∴AG=4﹣1=3,∴S△AOB=S△AOG+S△ABG=
,4),∴AG=4﹣1=3,∴S△AOB=S△AOG+S△ABG=![]() ×3×3=
×3×3=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O逆时针方向旋转90°
得到△OA1B1 .
(1)线段A1B1的长是 , ∠AOA1的度数是;
(2)连结AA1 , 求证:四边形OAA1B1是平行四边形;
(3)求四边形OAA1B1的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料,数学家高斯在上学时曾经研究过这样一个问题,1+2+3+…+10=?经过研究,这个问题的一般性结论是1+2+3+…+n=
 n(n+1),其中n为正整数,现在我们来研究一个类似的问题:1×2+2×3+…+ n(n+1)=?
n(n+1),其中n为正整数,现在我们来研究一个类似的问题:1×2+2×3+…+ n(n+1)=?观察下面三个特殊的等式:
1×2=
 (1×2×3-0×1×2)
(1×2×3-0×1×2)2×3=
 (2×3×4-1×2×3)
(2×3×4-1×2×3)3×4=
 (3×4×5-2×3×4)
(3×4×5-2×3×4)将这三个等式的两边相加,可以得到1×2+2×3+3×4=
 ×3×4×5=20.
×3×4×5=20.读完这段材料,请你计算:
(1)1×2+2×3+…+100×101;
(2)1×2+2×3+…+ n(n+1);
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过点C(1,2)分别作x轴,y轴的平行线,交直线y=-x+6于点A,B,若反比例函数y=
 (x>0)的图象与△ABC有公共点,求k的取值范围.
(x>0)的图象与△ABC有公共点,求k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是由四条曲线围成的广告标志,建立平面直角坐标系,双曲线对应的函数表达式分别为y=-
 ,y=
,y= .现用四根钢条固定这四条曲线,这种钢条加工成长方形产品按面积计算,每单位面积25元,请你帮助工人师傅计算一下,所需钢条一共花多少钱?
.现用四根钢条固定这四条曲线,这种钢条加工成长方形产品按面积计算,每单位面积25元,请你帮助工人师傅计算一下,所需钢条一共花多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数图象如图所示,根据图象可得:

(1)抛物线顶点坐标;
(2)对称轴为
(3)当x=时,y有最大值是;
(4)当时,y随着x得增大而增大.
(5)当时,y>0. -
科目: 来源: 题型:
查看答案和解析>>【题目】将连续的奇数1,3,5,7,9,…,排成如图7所示的数阵.
(1)十字框中的五个数的和与中间数15有什么关系?
(2)设中间数为
 ,用式子表示十字框中五个数之和;
,用式子表示十字框中五个数之和;(3)若将十字框中上下左右移动,可框住另外五个数,这五个数的和还有这种规律吗?
(4)十字框中五个数之和能等于2005吗?若能,请写出这五个数;若不能,说明理由.

相关试题

