【题目】如图,在平面直角坐标系中,正比例函数y=kx(k>0)与反比例函数y= ![]() 的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为(m , 0).其中m>0.
的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为(m , 0).其中m>0.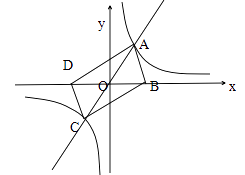
(1)四边形ABCD的是 . (填写四边形ABCD的形状)
(2)当点A的坐标为(n,3)时,四边形ABCD是矩形,求mn的值.
(3)试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.
参考答案:
【答案】
(1)平行四边形
(2)
解:因为A(n,3),且A在反比例函数y=![]() ,
,
则n=1,A (1,3).
∵ 四边形ABCD是矩形,
∴OB=OA=![]() ,
,
则m=![]() .
.
,∴mn=![]() .
.
(3)
不能.因为当四边形ABCD为菱形时,则AC⊥BD.
∵BD在x轴上,
∴AC在y轴上,
而反比例函数y=![]() 与y轴没有交点,
与y轴没有交点,
则随着k与m的变化,四边形ABCD不能成为菱形.
【解析】(1)由中心对称可知OA=OC,OB=OD,则四边形ABCD是平行四边形;
(2)可求出n的值;根据矩形的性质可得OA=OB,则可求出m;
(3)根据菱形的对角线互相垂直去判断.
【考点精析】关于本题考查的平行四边形的判定和菱形的性质,需要了解两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能得出正确答案.
-
科目: 来源: 题型:
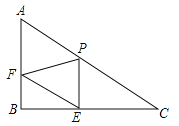
查看答案和解析>>【题目】已知Rt△ABC中,∠B=90°,AC=20,AB=10,P是边AC上一点(不包括端点A、C),过点P作PE⊥BC于点E,过点E作EF∥AC,交AB于点F.设PC=x,PE=y.
(1)求y与x的函数关系式;
(2)是否存在点P使△PEF是Rt△?若存在,求此时的x的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程(m+1)x2﹣3x+2=0是一元二次方程,则m的取值范围是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( )
A.两个直角三角形相似B.两个等腰三角形相似
C.两个等边三角形相似D.两个锐角三角形相似
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
 的图像交于(1,3),B(3,n)两点.
的图像交于(1,3),B(3,n)两点. 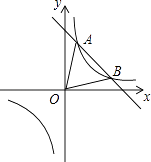
(1)求一次函数和反比例函数的解析式;
(2)连接AO,BO,求△ABO的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,线段BE上有一点C,以BC,CE为边分别在BE的同侧作等边三角形ABC,DCE,连接AE,BD,分别交CD,CA于Q,P.
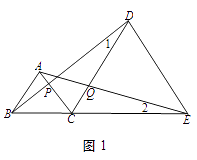
(1)找出图中的所有全等三角形.
(2)找出一组相等的线段,并说明理由.
(3)如图2,取AE的中点M、BD的中点N,连接MN,试判断三角形CMN的形状,并说明理由.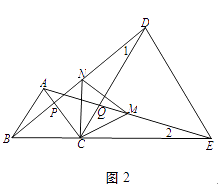
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在平行四边形ABCD中,点E在直线AD上,AE=
 AD,连接CE交BD于点F,则EF:FC的值是 .
AD,连接CE交BD于点F,则EF:FC的值是 .
相关试题

