【题目】如图,在边长为12cm的等边三角形ABC中,点P从点A开始沿AB边向点B以每秒钟1cm的速度移动,点Q从点B开始沿BC边向点C以每秒钟2cm的速度移动。若P、Q分别从A、B同时出发,其中任意一点到达目的地后,两点同时停止运动,求: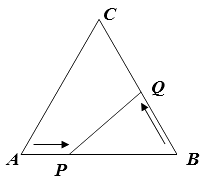
(1)经过6秒后,BP= cm,BQ=cm;
(2)经过几秒后,△BPQ是直角三角形?
(3)经过几秒△BPQ的面积等于 ![]() cm2 ?
cm2 ?
参考答案:
【答案】
(1)6;12
(2)
∵△ABC是等边三角形,
∴AB=AC=12cm,∠A=∠B=∠C=60°,
当∠PQB=90°时,
∴∠BPQ=30°,
∴BP=2BQ
∵BP=12-x,BQ=2x,
∴12-x=2×2x,
∴ ![]()
当∠QPB=90°时,
∴∠PQB=30°,
∴BQ=2PB,
∴2x=2(12-x),
x=6
答:6秒或 ![]() 秒时,△BPQ是直角三角形;
秒时,△BPQ是直角三角形;
(3)
作QD⊥AB于D,
∴∠QDB=90°,
∴∠DQB=30°,
∴DB =0.5 BQ=x,
在Rt△DBQ中,由勾股定理,得
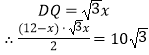
解得;x1=10,x2=2,
∵x=10时,2x>12,故舍去
∴x=2.
答:经过2秒△BPQ的面积等于 ![]() cm2
cm2
【解析】(1)解:由题意,得
AP=6cm,BQ=12cm.
∵△ABC是等边三角形
∴AB=BC=12cm,
∴BP=12-6=6cm.
【考点精析】根据题目的已知条件,利用等边三角形的性质和勾股定理的概念的相关知识可以得到问题的答案,需要掌握等边三角形的三个角都相等并且每个角都是60°;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=2(x﹣1)2+3可以看作是由抛物线y=2x2经过以下哪种变换得到的( )
A. 向左平移1个单位,再向上平移3个单位
B. 向右平移1个单位,再向上平移3个单位
C. 向左平移1个单位,再向下平移3个单位
D. 向右平移1个单位,再向下平移3个单位
-
科目: 来源: 题型:
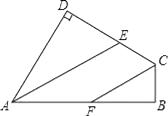
查看答案和解析>>【题目】如图在四边形ABCD中,∠B=∠D=90°,AE、CF分别平分∠BAD和∠BCD.试问直线AE、CF的位置关系如何?请说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
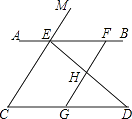
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=100°,∠D=30°,求∠AEM的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】在│-2│,-│0│,(-2)5,-│-2│,-(-2)这5个数中负数共有 ( )
A.1 个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】请写出一个含有两个字母、系数为﹣2的二次单项式 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是( )

A.①②③
B.①②
C.①③
D.②③
相关试题

