【题目】解下列方程:
(1)10﹣4(x+3)=2(x﹣1)
(2)![]() +
+ ![]() =1.
=1.
参考答案:
【答案】
(1)解:去括号,得10﹣4x﹣12=2x﹣2,
移项,得﹣4x﹣2x=﹣2﹣10+12
合并同类项,得﹣6x=0,
系数化为1,得x=0
(2)解:去分母,得2(2x﹣5)+3(3﹣x)=12
去括号,得4x﹣10+9﹣3x=12
移项,得4x﹣3x=12+10﹣9
合并同类项,得x=13
【解析】(1)根据去括号、移项、合并同类项、系数化为1,可得答案;(2)根据去分母、去括号、移项、合并同类项,可得答案.
【考点精析】通过灵活运用解一元一次方程的步骤,掌握先去分母再括号,移项变号要记牢.同类各项去合并,系数化“1”还没好.求得未知须检验,回代值等才算了即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,李老师出示了如下的题目:
“在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图,试确定线段AE与DB的大小关系,并说明理由”.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与DB的大小关系,请你直接写出结论:AEDB(填“>”,“<”或“=”).
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).理由如下:如图2,过点E作EF∥BC,交AC于点F.(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,CD= (请你直接写出结果).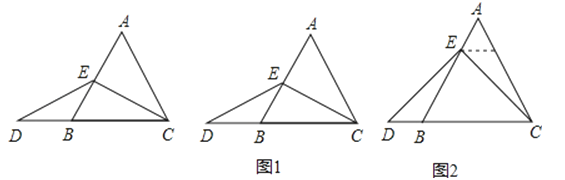
-
科目: 来源: 题型:
查看答案和解析>>【题目】如何作出一个图形的中心对称图形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形OABC为正方形,边长为6,点A、C分别在x轴,y轴的正半轴上,点D在OA上,且D点的坐标为(2,0),P是OB上的一个动点,试求PD+PA和的最小值是
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知n为正整数,且x2n=2,求(2x3n)2+(﹣x2n)3的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线AB上一点O,∠AOD=42°,∠BOC=34°,∠DOE=90°,OF平分∠COD,求∠FOD与∠EOB的度数.
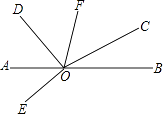
-
科目: 来源: 题型:
查看答案和解析>>【题目】若﹣9x2ym与xny是同类项,则m+n的值为( )
A. 0 B. 1 C. 2 D. 3
相关试题

