【题目】数学课上,李老师出示了如下的题目:
“在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图,试确定线段AE与DB的大小关系,并说明理由”.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与DB的大小关系,请你直接写出结论:AEDB(填“>”,“<”或“=”).
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).理由如下:如图2,过点E作EF∥BC,交AC于点F.(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,CD= (请你直接写出结果).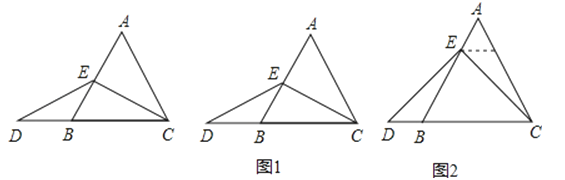
参考答案:
【答案】=;=;3或1.
【解析】解:(1)故答案为:=.
(2)过E作EF∥BC交AC于F,
∵等边三角形ABC,
∴∠ABC=∠ACB=∠A=60°,AB=AC=BC,
∴∠AEF=∠ABC=60°,∠AFE=∠ACB=60°,
即∠AEF=∠AFE=∠A=60°,
∴△AEF是等边三角形,
∴AE=EF=AF,
∵∠ABC=∠ACB=∠AFE=60°,
∴∠DBE=∠EFC=120°,∠D+∠BED=∠FCE+∠ECD=60°,
∵DE=EC,
∴∠D=∠ECD,
∴∠BED=∠ECF,
在△DEB和△ECF中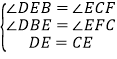 ,
,
∴△DEB≌△ECF,
∴BD=EF=AE,
即AE=BD,
故答案为:=.
(3)解:CD=1或3,
理由是:分为两种情况:①如图1
过A作AM⊥BC于M,过E作EN⊥BC于N,
则AM∥EN,
∵△ABC是等边三角形,
∴AB=BC=AC=1,
∵AM⊥BC,
∴BM=CM=![]() BC=
BC=![]() ,
,
∵DE=CE,EN⊥BC,
∴CD=2CN,
∵AM∥EN,
∴△AMB∽△ENB,
∴![]() ,
,
∴![]()
∴BN=![]() ,
,
∴CN=1+![]() =
=![]() ,
,
∴CD=2CN=3;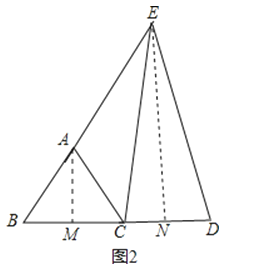
②如图2,作AM⊥BC于M,过E作EN⊥BC于N,
则AM∥EN,
∵△ABC是等边三角形,
∴AB=BC=AC=1,
∵AM⊥BC,
∴BM=CM=![]() BC=
BC=![]() ,
,
∵DE=CE,EN⊥BC,
∴CD=2CN,
∵AM∥EN,
∴![]()
∴![]()
∴MN=1,
∴CN=1﹣![]() =
=![]() ,
,
∴CD=2CN=1,
即CD=3或1.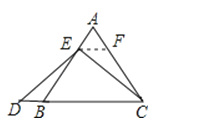
(1)根据等边三角形性质和等腰三角形的性质求出∠D=∠ECB=30°,求出∠DEB=30°,求出BD=BE即可;
(2)过E作EF∥BC交AC于F,求出等边三角形AEF,证△DEB和△ECF全等,求出BD=EF即可;
(3)当D在CB的延长线上,E在AB的延长线式时,由(2)求出CD=3,当E在BA的延长线上,D在BC的延长线上时,求出CD=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】全等的两个图形一定关于中心对称吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】26个大写英文字母中有多少个是中心对称图形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知同一平面内∠AOB=90°,∠AOC=60°,

(1)填空∠BOC=;
(2)如OD平分∠BOC,OE平分∠AOC,直接写出∠DOE的度数为°;
(3)试问在(2)的条件下,如果将题目中∠AOC=60°改成∠AOC=2α(α<45°),其他条件不变,你能求出∠DOE的度数吗?若能,请你写出求解过程;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如何作出一个图形的中心对称图形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形OABC为正方形,边长为6,点A、C分别在x轴,y轴的正半轴上,点D在OA上,且D点的坐标为(2,0),P是OB上的一个动点,试求PD+PA和的最小值是
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)10﹣4(x+3)=2(x﹣1)
(2)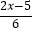 +
+ 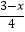 =1.
=1.
相关试题

