【题目】（10分）如图，抛物线与x轴交于点A和点B（1，0），与y轴交于点C（0，3），其对称轴l为．

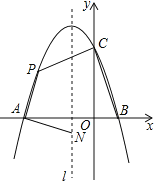
（1）求抛物线的解析式并写出其顶点坐标；

（2）若动点P在第二象限内的抛物线上，动点N在对称轴l上．

①当PA⊥NA，且PA=NA时，求此时点P的坐标；

②当四边形PABC的面积最大时，求四边形PABC面积的最大值及此时点P的坐标．

参考答案：

【答案】（1），（﹣1，4）；（2）①P（，2）；②，P（， ）．

【解析】试题分析：（1）将B、C的坐标代入已知的抛物线的解析式，由对称轴为即可得到抛物线的解析式；

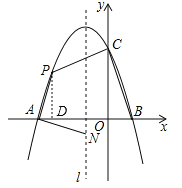
（2）①首先求得抛物线与x轴的交点坐标，然后根据已知条件得到PD=OA，从而得到方程求得x的值即可求得点P的坐标；

②，表示出来得到二次函数，求得最值即可．

试题解析：（1）∵抛物线与x轴交于点A和点B（1，0），与y轴交于点C（0，3），其对称轴l为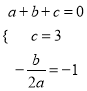，∴，解得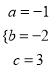： ，∴二次函数的解析式为=，∴顶点坐标为（﹣1，4）；

（2）令，解得或，∴点A（﹣3，0），B（1，0），作PD⊥x轴于点D，∵点P在上，∴设点P（x， ），

①∵PA⊥NA，且PA=NA，∴△PAD≌△AND，∴OA=PD，即，解得x=（舍去）或x=，∴点P（，2）；

②设P(x，y)，则，∵

=OBOC+ADPD+ (PD+OC)OD==

===，

∴当x=时， =，当x=时， =，此时P（， ）．

关闭