Question

【题目】探究：如图1，直线l与坐标轴的正半轴分别交于A，B两点，与反比例函数y= （k＞0，x＞0）的图象交于C，D两点（点C在点D的左边），过点C作CE⊥y轴于点E，过点D作DF⊥x轴于点F，CE与DF交于点G（a，b）．

（1）若 ，请用含n的代数式表示 ；
（2）求证：AC=BD；
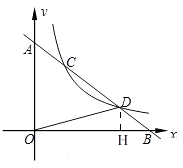
应用：如图2，直线l与坐标轴的正半轴分别交于点A，B两点，与反比例函数y= （k＞0，x＞0）的图象交于点C，D两点（点C在点D的左边），已知 ，△OBD的面积为1，试用含m的代数式表示k．

Answer 1

【答案】
（1）解：∵∠ACE=∠DCG，∠AEC=∠DGC=90°，

∴△ACE∽△DCG

∴

（2）解：∵G（a，b）

∴C（ ） D（a， ），

∴EC= ，CG=a﹣ ，DF= ，DG=b﹣ ，

∴ ，

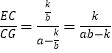由（1）知，△ACE∽△DCG，

∴ = ，

同理：△DCG∽△DBF，

∴ ，

即△ACE与△DBF都和△DCG相似，且相似比都为 ，

∴△ACE≌△DBF

∴AC=BD，

应用：如图，过点D作DH⊥x轴于点H

由（2）可得AC=BD

∵ ，

∴ ，

∴ ，

又∵ ，

∴ ，

∴ ，

∴ ．

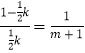【解析】（1）利用两角相等的两三角形相似即可得出结论；（2）先求出 ， ，进而判断出△ACE≌△DBF即可得出结论；

应用：先求出 ，进而得出 ，即可得出结论．