【题目】如图,坡AB的坡比为1:2.4,坡长AB=130米,坡AB的高为BT.在坡AB的正面有一栋建筑物CH,点H、A、T在同一条地平线MN上.

(1)试问坡AB的高BT为多少米?
(2)若某人在坡AB的坡脚A处和中点D处,观测到建筑物顶部C处的仰角分别为60°和30°,试求建筑物的高度CH.(精确到米, ![]() ≈1.73,
≈1.73, ![]() ≈1.41)
≈1.41)
参考答案:
【答案】(1)坡AB的高BT为50米;(2)建筑物高度为89米
【解析】试题分析:(1)根据坡AB的坡比为1:2.4,可得tan∠BAT=![]() ,可设TB=h,则AT=2.4h,由勾股定理可得
,可设TB=h,则AT=2.4h,由勾股定理可得![]() ,即可求解,(2) 作DK⊥MN于K,作DL⊥CH于L, 在△ADK中,AD=
,即可求解,(2) 作DK⊥MN于K,作DL⊥CH于L, 在△ADK中,AD=![]() AB=65,KD=
AB=65,KD=![]() BT=25,得AK=60,在△DCL中,∠CDL=30°,令CL=x,得LD=
BT=25,得AK=60,在△DCL中,∠CDL=30°,令CL=x,得LD= ![]() , 易知四边形DLHK是矩形,则LH=DK,LD=HK,在△ACH中,∠CAH=60°,CH=x+25,得AH=
, 易知四边形DLHK是矩形,则LH=DK,LD=HK,在△ACH中,∠CAH=60°,CH=x+25,得AH=![]() , 所以
, 所以![]() ,解得
,解得![]() ,则CH=
,则CH=![]() .
.
试题解析:(1)在△ABT中,∠ATB=90°,BT:AT=1:2.4,AB=130,
令TB=h,则AT=2.4h,
有![]() ,
,
解得h=50(舍负).
答:坡AB的高BT为50米.
(2)作DK⊥MN于K,作DL⊥CH于L,
在△ADK中,AD=![]() AB=65,KD=
AB=65,KD=![]() BT=25,得AK=60,
BT=25,得AK=60,
在△DCL中,∠CDL=30°,令CL=x,得LD= ![]() ,
,
易知四边形DLHK是矩形,则LH=DK,LD=HK,
在△ACH中,∠CAH=60°,CH=x+25,得AH=![]() ,
,
所以![]() ,解得
,解得![]() ,
,
则CH=![]() .
.
答:建筑物高度为89米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x、y的方程组
 的解都小于1,若关于a的不等式组
的解都小于1,若关于a的不等式组 恰好有三个整数解.
恰好有三个整数解.(1)分别求出m与n的取值范围;
(2)化简:

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了迎接“十一”小长假的购物高峰.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:
运动鞋
价格甲
乙
进价(元/双)
m
m﹣20
售价(元/双)
240
160
已知:用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.
(1)求m的值;
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)不少于21700元,且不超过22300元,问该专卖店有几种进货方案?
(3)在(2)的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠a(50<a<70)元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1,在平面直角坐标系xOy中,直线l1,l2都经过点A(﹣6,0),它们与y轴的正半轴分别相交于点B,C,且∠BAO=∠ACO=30

(1)求直线l1,l2的函数表达式;
(2)设P是第一象限内直线l1上一点,连接PC,有S△ACP=24
 .M,N分别是直线l1,l2上的动点,连接CM,MN,MP,求CM+MN+NP的最小值;
.M,N分别是直线l1,l2上的动点,连接CM,MN,MP,求CM+MN+NP的最小值;(3)如图2,在(2)的条件下,将△ACP沿射线PA方向平移,记平移后的三角形为△A′C′P′,在平移过程中,若以A,C',P为顶点的三角形是等腰三角形,请直接写出所有满足条件的点C′的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是人字型金属屋架的示意图,该屋架由BC、AC、BA、AD四段金属材料焊接而成,其中A、B、C、D四点均为焊接点,且AB=AC,D为BC的中点,假设焊接所需的四段金属材料已截好,并已标出BC段的中点D,那么,如果焊接工身边只有可检验直角的角尺,而又为了准确快速地焊接,他应该首先选取的两段金属材料及焊接点是( )
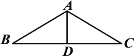
A.AB和AD,点AB.AB和AC,点B
C.AC和BC, 点CD.AD和BC,点D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=4,BC=3,D是边AC的中点,CE⊥BD交AB于点E.
(1)求tan∠ACE的值;
(2)求AE:EB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( )
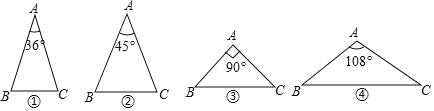
A. ①③B. ①②④C. ①③④D. ①②③④
相关试题

