【题目】图1,在平面直角坐标系xOy中,直线l1,l2都经过点A(﹣6,0),它们与y轴的正半轴分别相交于点B,C,且∠BAO=∠ACO=30![]()
(1)求直线l1,l2的函数表达式;
(2)设P是第一象限内直线l1上一点,连接PC,有S△ACP=24![]() .M,N分别是直线l1,l2上的动点,连接CM,MN,MP,求CM+MN+NP的最小值;
.M,N分别是直线l1,l2上的动点,连接CM,MN,MP,求CM+MN+NP的最小值;
(3)如图2,在(2)的条件下,将△ACP沿射线PA方向平移,记平移后的三角形为△A′C′P′,在平移过程中,若以A,C',P为顶点的三角形是等腰三角形,请直接写出所有满足条件的点C′的坐标.

参考答案:
【答案】(1)直线l2的解析式为![]() ,直线l1的解析式为
,直线l1的解析式为![]() ;(2)
;(2)![]() ;(3) (﹣9﹣3
;(3) (﹣9﹣3![]() ,3
,3![]() ﹣
﹣![]() )或(﹣3,5
)或(﹣3,5![]() )或(3﹣3
)或(3﹣3![]() ,7
,7![]() ﹣
﹣![]() )
)
【解析】
(1)求出B,C两点坐标利用待定系数法即可解决问题.
(2)如图1中,设点P(m,![]() m+2
m+2![]() ),利用三角形的面积公式求出点P坐标,如图1﹣1中,作点C关于直线AP的对称点C′,点P关于直线AC的对称点P′,连接P′C′交AP于M′,交AC于N′,此时CM′+M′N′+N′P的值最小,最小值是线段P′C′的长.
),利用三角形的面积公式求出点P坐标,如图1﹣1中,作点C关于直线AP的对称点C′,点P关于直线AC的对称点P′,连接P′C′交AP于M′,交AC于N′,此时CM′+M′N′+N′P的值最小,最小值是线段P′C′的长.
(3)由题意,点C的运动轨迹是直线y=![]() x+6
x+6![]() ,设C′(a,
,设C′(a,![]() a+6
a+6![]() ).分三种情形:①当AC′=AP=8
).分三种情形:①当AC′=AP=8![]() 时.②当C′A=C′P时.③当PA=PC′=8
时.②当C′A=C′P时.③当PA=PC′=8![]() 时,分别求解即可解决问题.
时,分别求解即可解决问题.
解:(1)如图1中,

∵A(﹣6,0),
∴OA=6,
∵∠AOB=90°,∠ACO=∠BAO=30°,
∴OC=![]() OA=6
OA=6![]() ,OB=
,OB=![]() OA=2
OA=2![]() ,
,
∴C(0,6![]() ),B(O,2
),B(O,2![]() ),
),
∴直线l2的解析式为y=![]() x+6
x+6![]() ,直线l1的解析式为y=
,直线l1的解析式为y=![]() x+2
x+2![]() .
.
(2)设点P(m,![]() m+2
m+2![]() ),∵S△APC=S△ABC+S△BCP,
),∵S△APC=S△ABC+S△BCP,
∴![]() BC(xP﹣xA)=24
BC(xP﹣xA)=24![]() ,
,
∴![]() ×4
×4![]() ×(m+6)=24
×(m+6)=24![]() ,
,
解得m=6,
∴P(6,4![]() ),
),
如图1﹣1中,作点C关于直线AP的对称点C′,点P关于直线AC的对称点P′,连接P′C′交AP于M′,交AC于N′,此时CM′+M′N′+N′P的值最小,最小值是线段P′C′的长.

∵∠CAP=∠PAO=30°,
∴点C′在x轴上,AC′=AC=12,
∵∠CAP′=∠PAC=∠PAO=30°,
∴∠P′AC′=90°,PA=P′A=8![]() ,
,
∴P′C′=![]() =
=![]() =4
=4![]() ,
,
∴CM+MN+NP的最小值为4![]() .
.
(3)如图2中,

由题意,点C的运动轨迹是直线y=![]() x+6
x+6![]() ,设C′(a,
,设C′(a,![]() a+6
a+6![]() ).
).
①当AC′=AP=8![]() 时,(a+6)2+(
时,(a+6)2+(![]() a+6
a+6![]() )2=(8
)2=(8![]() )2,
)2,
解得a=﹣9﹣3![]() 或﹣9+3
或﹣9+3![]() (舍弃),
(舍弃),
∴C′(﹣9﹣3![]() ,3
,3![]() ﹣
﹣![]() ).
).
②当C′A=C′P时,(a+6)2+(![]() a+6
a+6![]() )2=(a﹣6)2+(
)2=(a﹣6)2+(![]() a+6
a+6![]() ﹣4
﹣4![]() )2,
)2,
解得a=﹣3,
∴C′(﹣3,5![]() ).
).
③当PA=PC′=8![]() 时,(a﹣6)2+(
时,(a﹣6)2+(![]() a+6
a+6![]() ﹣4
﹣4![]() )2=(8
)2=(8![]() )2,
)2,
解得a=3﹣3![]() 或3+3
或3+3![]() (舍弃)
(舍弃)
∴C′(3﹣3![]() ,7
,7![]() ﹣
﹣![]() )
)
综上所述,满足条件的点C′的坐标为(﹣9﹣3![]() ,3
,3![]() ﹣
﹣![]() )或(﹣3,5
)或(﹣3,5![]() )或(3﹣3
)或(3﹣3![]() ,7
,7![]() ﹣
﹣![]() ).
).
【点晴】
一次函数综合题,考查了待定系数法、轴对称变换、等腰三角形的判定和性质等知识,解题关键是学会利用转化的思想思考问题,学会用分类讨论的思想解决问题,学会构建方程解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1+∠2﹦180°,∠3﹦∠B,则DE∥BC,下面是王华同学的推导过程﹐请你帮他在括号内填上推导依据或内容.

证明:
∵∠1+∠2﹦180(已知),
∠1﹦∠4 (_________________),
∴∠2﹢_____﹦180°.
∴EH∥AB(___________________________________).
∴∠B﹦∠EHC(________________________________).
∵∠3﹦∠B(已知)
∴ ∠3﹦∠EHC(____________________).
∴ DE∥BC(__________________________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x、y的方程组
 的解都小于1,若关于a的不等式组
的解都小于1,若关于a的不等式组 恰好有三个整数解.
恰好有三个整数解.(1)分别求出m与n的取值范围;
(2)化简:

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了迎接“十一”小长假的购物高峰.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:
运动鞋
价格甲
乙
进价(元/双)
m
m﹣20
售价(元/双)
240
160
已知:用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.
(1)求m的值;
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)不少于21700元,且不超过22300元,问该专卖店有几种进货方案?
(3)在(2)的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠a(50<a<70)元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,坡AB的坡比为1:2.4,坡长AB=130米,坡AB的高为BT.在坡AB的正面有一栋建筑物CH,点H、A、T在同一条地平线MN上.

(1)试问坡AB的高BT为多少米?
(2)若某人在坡AB的坡脚A处和中点D处,观测到建筑物顶部C处的仰角分别为60°和30°,试求建筑物的高度CH.(精确到米,
 ≈1.73,
≈1.73,  ≈1.41)
≈1.41) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是人字型金属屋架的示意图,该屋架由BC、AC、BA、AD四段金属材料焊接而成,其中A、B、C、D四点均为焊接点,且AB=AC,D为BC的中点,假设焊接所需的四段金属材料已截好,并已标出BC段的中点D,那么,如果焊接工身边只有可检验直角的角尺,而又为了准确快速地焊接,他应该首先选取的两段金属材料及焊接点是( )
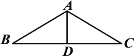
A.AB和AD,点AB.AB和AC,点B
C.AC和BC, 点CD.AD和BC,点D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=4,BC=3,D是边AC的中点,CE⊥BD交AB于点E.
(1)求tan∠ACE的值;
(2)求AE:EB.

相关试题

